Cho hình 36. Hãy viết hệ thức giữa:
Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
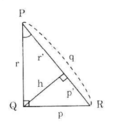
Hình 36
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông p, r và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
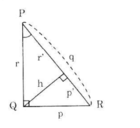
Hình 36
a) p 2 = p ' . q ; r 2 = r ' . q
![]()
c) h 2 = p ' . r '
Cho hình 36.
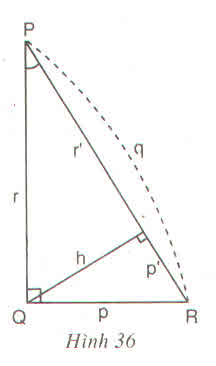
Hãy viết hệ thức giữa :
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền
b) Các cạnh góc vuong p, r và đường cao h
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
Cho hình 36. Hãy viết hệ thức giữa:
Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
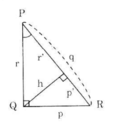
Hình 36
Cho hình 36. Hãy viết hệ thức giữa:
Các cạnh góc vuông p, r và đường cao h.
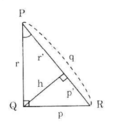
Hình 36
Cho tam giác vuông tại A đường cao AH
A. Hãy viết hệthức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền
B. Tính AH biết BH:4cm HC:9cm
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH.
a) Hãy viết hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền
b) Tính AH biết BH = 4cm; HC = 9cm
\(a,AH^2=BH.BC\)
\(b,\)Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\),đường cao \(AH\) có:
\(AH^2=BH.BC\)
\(\Rightarrow AH^2=4.9\)
\(\Rightarrow AH^2=36\Rightarrow AH=6\left(cm\right)\)
Cho tam giác ABC vuông tai A đường cao AH
A. Hãy viết hệ thức liên hệ giữa đường cao va hình chiếu của các cạch góc vuông trên canh huyền
B. Tinh AH biết BH=4cm HC=9cm
A. Hệ thức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền: \(AH^2=BH.CH\)
B. Ta có △ABC vuông tại A có đường cao AH\(\Rightarrow AH^2=BH.CH=4.9=36\Rightarrow AH=6\left(cm\right)\)
Cho tam giác ABC vuông tại A , kẻ đường cao AH.Biết hai cạnh góc vuông là 7 và 8.Tính độ dài cạnh huyền và hình chiếu của các cạnh góc vuông trên cạnh huyền.
1) Một tam giác vuông có canh huyền là 5 và đường cao ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
2) Cho một tam giác vuông. Biết tỉ số hai cạnh góc vuông là 3:4 và cạnh huyền là 125 cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.
câu 2
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5
1) Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5