\(a,AH^2=BH.BC\)
\(b,\)Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\),đường cao \(AH\) có:
\(AH^2=BH.BC\)
\(\Rightarrow AH^2=4.9\)
\(\Rightarrow AH^2=36\Rightarrow AH=6\left(cm\right)\)
\(a,AH^2=BH.BC\)
\(b,\)Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\),đường cao \(AH\) có:
\(AH^2=BH.BC\)
\(\Rightarrow AH^2=4.9\)
\(\Rightarrow AH^2=36\Rightarrow AH=6\left(cm\right)\)
Cho tam giác vuông tại A đường cao AH
A. Hãy viết hệthức liên hệ giữa đường cao và hình chiếu của các cạnh góc vuông trên cạnh huyền
B. Tính AH biết BH:4cm HC:9cm
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
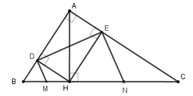
Tính độ dài đoạn thẳng DE
A. DE = 5cm
B. DE = 8cm
C. DE = 7cm
D. DE = 6cm
Cho một tam giác ABC vuông tại A có \(\widehat{B}=\dfrac{1}{2}\widehat{C}\). Kẻ đường cao AH sao cho cạnh AH vuông góc với cạnh huyền BC tại H. Các hình chiếu của AB và AC trên BC lần lượt là BH và HC. Biết HC = 1,6cm.
a) Tính góc B và C, và các tỉ số lượng giác của chúng nó.
b*) Tính độ dài các cạnh BC, AB và AC.
Gợi ý: Sử dụng các hệ thức về tỉ số lượng giác của góc nhọn và một trong bốn hệ thức về cạnh góc vuông và đường cao trong tam giác vuông để tính.
c) Tính độ dài các cạnh AH và BH.
d) Hãy chứng minh rằng: Cả ba tam giác vuông ABC, HBA và HAC đồng dạng với nhau.
e*) Chứng minh rằng: \(\dfrac{\sin\widehat{HAC}}{\cos\widehat{HBA}}\div\dfrac{\tan\widehat{HAC}}{\cot\widehat{ABC}}=\dfrac{csc^2\widehat{ABC}}{sec^2\widehat{ABC}\cdot\cot\widehat{HBA}}\)
Gợi ý:
1. Secant - sec α nghịch đảo với cos α
2. Cosecant - csc α nghịch đảo với sin α
cho tam giác ABC vuông tại A, đường cao AH . Cho biết BH = 4cm , CH = 9cm, DE = 6 cm. Gọi D. E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC
a) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N. CMinh MN = 1/2 BC
b) Tính S tứ giác DENM
Cho D ABC vuông tại A có AB = 6cm, AC = 8cm, BC = 10cm, đường cao AH a) Viết các hệ thức giữa cạnh và đường cao AH trong tam giác ABC. b) Tính AH, BH, CH
Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
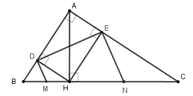
Tính độ dài đoạn thẳng DE.
A. DE = 12cm
B. DE = 8cm
C. DE = 15cm
D. DE = 6cm
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông p, r và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
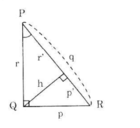
Hình 36
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 4cm, CH= 9cm. Gọi D,E lần lượt là hình chiếu vuông góc của H trên cạch AB và AC
a) Tứ giác ADHE là hình gì, tại sao? Tính DE
b) Các đường thẳng vuông góc DE tại D và E lần lượt cắt BC tại M và N. C/m MN=1/2BC
c) Tính diện tích tứ giác DEMN
d) C/m AD.AB=AE.AC
Cho tam giác ABC vuông tại A đường cao AH. Gọi D và E lần lượt là hinh chiếu của H trên AB,BC. Biết BH=4cm HC=9cm
a) Các đường thẳng vuông góc với DE tại D và E cắt BC tại M và N. Chứng minh M là trung điểm của BH
b) Tính diện tích tam giác DEMN