Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Nếu AB = CD thì OH = OK.
Những câu hỏi liên quan
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
a) Nếu AB = CD thì OH = OK.
b) Nếu OH = OK thì AB = CD.
OH là một phần đường kính vuông góc với dây AB
⇒ H là trung điểm của AB ⇒ AB = 2HB
OK là một phần đường kính vuông góc với dây CD
⇒ K là trung điểm của CD ⇒ CD = 2KD
Theo mục 1: OH2 + HB2= OK2+ KD2
a) Ta có: AB = CD ⇒ HB = KD
⇒ OH2 = OK2 ⇒ OH = OK
b) Ta có: OH = OK ⇒ HB2 = KD2
⇒ HB = KD ⇒ AB = CD
Đúng 0
Bình luận (0)
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Nếu OH = OK thì AB = CD.
Ta có: OH = OK ⇒ HB2 = KD2
⇒ HB = KD ⇒ AB = CD
Đúng 0
Bình luận (0)
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài:
a) OH và OK, nếu biết AB > CD.
b) AB và CD, nếu biết OH < OK.
a) Nếu AB > CD thì HB > KD
⇒ HB2 > KD2
Mà : OH2 + HB2 = OK2 + KD2
⇒ OH2 < OK2
⇒ OH < OK
b) Nếu OH < OK thì OH2 < OK2
⇒ HB2 > KD2 ⇒ HB > KD
⇒ AB > CD
Đúng 0
Bình luận (0)
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài: AB và CD, nếu biết OH < OK.
Nếu OH < OK thì OH2 < OK2
⇒ HB2 > KD2 ⇒ HB > KD
⇒ AB > CD
Đúng 0
Bình luận (0)
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài:
OH và OK, nếu biết AB > CD.
Nếu AB > CD thì HB > KD
⇒ HB2 > KD2
Mà : OH2 + HB2 = OK2 + KD2
⇒ OH2 < OK2
⇒ OH < OK
Đúng 0
Bình luận (0)
Hãy sừ dụng kết quq của bài toán mục 1 để so sánh các độ dài :
a. OH và OK nếu biết AB > CD
b. AB và CD nếu biết OH<OK
Cho đường tròn (O;5). Vẽ 2 dây AB = 6cm và CD = 8cm. So sánh khoảng cách từ tâm O đến 2 dây AB và CD. HD: Kẻ OH^AB (OH là khoảng cách từ O đến AB); OK^CD (OK là khoảng cách từ O đến CD) Sử dụng định lí 2 bài 2 và định lí Py – ta – go để tính OH và OK.
Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:AG 2/3 AD
Đọc tiếp
Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:
AG = 2/3 AD
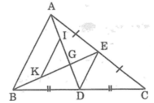
Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD
Đúng 0
Bình luận (0)
Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:IK // DE, IK DE
Đọc tiếp
Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:
IK // DE, IK = DE
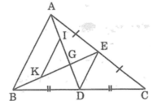
Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:
DE // AB và DE = 1/2 AB (1)
IK // AB và IK = 1/2 AB (2)
Từ (1) và (2) suy ra:
DE // IK và DE = IK.
Đúng 0
Bình luận (0)