a) Nếu AB > CD thì HB > KD
⇒ HB2 > KD2
Mà : OH2 + HB2 = OK2 + KD2
⇒ OH2 < OK2
⇒ OH < OK
b) Nếu OH < OK thì OH2 < OK2
⇒ HB2 > KD2 ⇒ HB > KD
⇒ AB > CD
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài: AB và CD, nếu biết OH < OK.
Hãy sử dụng kết quả của bài toán ở mục 1 để so sánh các độ dài:
OH và OK, nếu biết AB > CD.
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
a) Nếu AB = CD thì OH = OK.
b) Nếu OH = OK thì AB = CD.
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Nếu AB = CD thì OH = OK.
Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
Nếu OH = OK thì AB = CD.
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
OH và OK
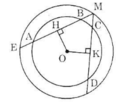
Hình 70
Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
a) OH và OK
b) ME và MF
c) MH và MK.
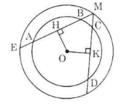
Hình 70
Cho(O;R), 2 dây AB, CD. OH vuông góc với AB tại H. OK vuông góc với CD tại K.
CMR:
a) Nếu AB=CD thì OH=OK
b) Nếu OH=OK thì AB=CD
c) Nếu OH>OK thì AB<CD
Tam giác ABC nội tiếp đường tròn (O) có ∠ A > ∠ B > ∠ C. Gọi OH, OI, OK theo thứ tự là khoảng cách từ O đến BC, AC, AB. So sánh các độ dài OH, OI, OK.
