a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có

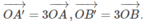
Vì  O A →   =   ( 0 ; 4 ) nên  O A ' →   =   ( 0 ; 12 ) . Do đó A′ = (0;12).

Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:

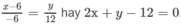
b) Có thể giải tương tự như câu a) .

Sau đây ta sẽ giải bằng cách khác.

Vì d 2   / /   d nên phương trình của d 2  có dạng 2x + y + C = 0.

Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:

I A ' →   =   − 2 I A →  hay x′ + 1 = −2, y′ − 2 = −4

Suy ra x′ = −3, y′ = −2

Do A' thuộc d 2  nên 2.(−3) – 2 + C = 0.

Từ đó suy ra C = 8

Phương trình của d 2  là 2x + y + 8 = 0

Gọi các đồ thị có CT chung là \(ax+b\)

\(a,\Leftrightarrow\left\{{}\begin{matrix}-a+b=-5\\a=0;b\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-5\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=-5\\ b,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\a=2;b\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\Leftrightarrow\left(d_2\right):y=2x+7\\ c,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\2a=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=3\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=-2x+3\\ d,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b=0\end{matrix}\right.\Leftrightarrow\left(d_4\right):y=-5x\)

a: Vì Δ//d nên Δ: 3x-4y+c=0

Thay x=1 và y=4 vào Δ, ta được:

c+3-16=0

=>c=13

b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0

Thay x=-3 và y=-5 vào Δ, ta được:

c+4*(-3)+3(-5)=0

=>c-27=0

=>c=27

=>4x+3y+27=0

5:

Gọi (d): y=ax+b là phương trình cần tìm

Theo đề, ta có hệ:
3a+b=-1 và 2a+b=3

=>a=-4 và b=11

=>y=-4x+11

4:

vecto BC=(1;-1)

=>AH có VTPT là (1;-1)

Phương trình AH là:

1(x-1)+(-1)(y+3)=0

=>x-1-y-3=0

=>x-y-4=0

a) d 1 : 3x + 2y + 6 = 0

b) Giao của d và Δ là A(2;0). Lấy B(0; −3) thuộc d. Ảnh của B qua phép đối xứng của đường thẳng Δ là B′(5;2). Khi đó d' chính là đường thẳng AB′: 2x − 3y – 4 = 0

Ta có: \(\Delta//d\Rightarrow\Delta:2x-3y+c=0\left(c\ne-1\right)\)

\(A\left(1;2\right)\in\Delta:2\cdot1-3\cdot2+c=0\)

\(\Leftrightarrow c=4\)

Vậy: \(\Delta:2x-3y+4=0\)

Vì (Δ)//d nên Δ: 2x-3y+c=0

Thay x=1 và y=2 vào Δ, ta được:

c+2-6=0

=>c=4

Lấy một điểm thuộc d, chẳng hạn M = (0; 1).

Khi đó M′ = T v → ( M ) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'.

Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0.

Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 .

Do đó d' có phương trình 2x − 3y + 10 = 0.

a: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)

\(a,\text{PT hoành độ giao điểm: }2x+3=-3x-2\Leftrightarrow x=-1\Leftrightarrow y=1\Leftrightarrow A\left(-1;1\right)\\ b,\text{Gọi đt đó là }y=ax+b\\ \Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\a=-1;b\ne5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\Leftrightarrow y=-x\\ d,\text{Gọi đt cần tìm là }y=ax+b\\ \Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\Leftrightarrow y=-2x-1\)

a: Tọa độ giao điểm là:

\(\left\{{}\begin{matrix}2x+3=-3x-2\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)