Nếu góc lượng giác có s đ O x , O z = - 63 π 2 thì hai tia Ox và Oz
A. Trùng nhau.
B. Vuông góc.
C. Tạo với nhau một góc bằng 3π/4.
D. Đối nhau.
Cho một góc lượng giác $(O x, O u)$ có số đo $240^{\circ}$ và một góc lượng giác $(O x, O v)$ có số đo $-270^{\circ}$. Tính số đo của các góc lượng giác $(O u, O v)$.
Số đo của các góc lượng giác tia đầu $O u$, tia cuối $O v$ là
\(sđ(O u, O v) = sđ(O x, O v) - sđ(O x, O u)+ k{360}^{\circ}(k \in \mathbb{Z}) \)
\(=-270^{\circ}-240^{\circ}+k 360^{\circ}=-510^{\circ}+k 360^{\circ} \)
\( =-150^{\circ}+(k-1) 360^{\circ}=-150^{\circ}+n 360^{\circ} \quad(n=k-1, n \in \mathbb{Z})
\)
Vậy các góc lượng giác $(O u, O v)$ có số đo là $-150^{\circ}+n 360^{\circ} \quad(n \in \mathbb{Z})$.
Đúng ghi Đ, sai ghi S vào ô trống
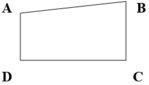
a.Tứ giác ABCD có cạnh AB vuông góc với cạnh BC. o
b.Tứ giác ABCD có cạnh AD song song với cạnh BC. o
Cho hai góc nhọn xOy và x'O'y' có các cạnh tương ứng Ox // O'x' , Oy // O'y'. Vẽ các tia Oz và O'z' lần lượt là phân giác của góc xOy và x'O'y'. Chứng tỏ :
a) Hai góc xOy và x'O'y' bằng nhau.
b) Oz // O'z'.
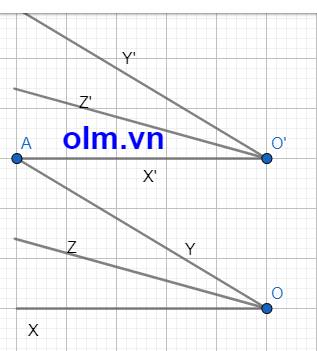
a,Kéo dài OY cắt O'X' tại A ta có:
\(\widehat{XOY}\) = \(\widehat{XOA}\) = \(\widehat{OAO'}\) (so le trong) (1)
\(\widehat{Y'O'X'}\) = \(\widehat{Y'O'A}\) = \(\widehat{OAO'}\) (so le trong) (2)
Kết hợp (1) Và (2) ta có:
\(\widehat{XOY=}\) \(\widehat{X'O'Y'}\) (đpcm)
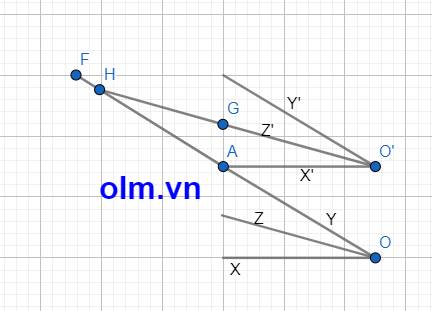
b, Kéo dài OY cắt O'Z' tại H
\(\widehat{ZOA}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\) (vì OZ là phân giác của góc XOY
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{X'O'Y'}\) (vì OY là phân giác của góc X'O'Y')
Mặt khác ta có \(\widehat{OAO'}\) = \(\widehat{HO'A}\) + \(\widehat{AHO'}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó)
\(\widehat{HO'A}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) ⇒ \(\widehat{AHO'}\) = \(\dfrac{1}{2}\) \(\widehat{OAO'}\) = \(\dfrac{1}{2}\) \(\widehat{XOY}\)
⇒ \(\widehat{ZOA}\) = \(\widehat{AHO'}\) (hai góc này ở vị trí so le trong)
⇒ OZ // O'Z' (đpcm)
Trên nửa mặt phẳng bờ chứa tia Ox vẽ các tia Oy o Z Ot sao cho x O y = 80 độ yo z = 30 độ Vẽ tia Ot là tia phân giác của góc yOz Tính góc x o t
Cho tia Oz là p/g \(\widehat{xOy}\) lấy D c Oz. Kẻ DH vuông góc với Ox (H c Ox). Kẻ DK vuông góc với Oy (K c Oy)
a) CM: Tam giác ODH = tam giác ODK
b) HB cắt tia Oy tại A, KD cắt tia Ox tại B. CM: tam giác HDB = tam giác KDA
c) CM: OA = OB
Bài 2.Các câu sau đúng hay sai:
Câu 1: Hai góc cùng bù với góc thứ ba thì bù nhau.
Câu 2: Nếu hai đại lượng x tỷ lệ nghịch với đại lượng y, đại lượng y tỷ lệ nghịch với đại lượng z thì
đại lượng x tỷ lệ thuận với đại lượng z.
Câu 3: Hai tam giác có hai cặp góc và 1 cặp cạnh bằng nhau thì hai tam giác đó bằng nhau.
Câu 4: Một điểm nằm trên trục hoành thì có hoành độ bằng 0.
Mọi người có thể giải giúp em bằng phương pháp S*O*S hoặc là bán S*O*S - bán Schur được không ạ? Nếu không thì dùng BĐT AM-GM hoặc các bđt khác cũng được ạ!
Cho x, y, z là các số thực dương. Chứng minh rằng: \(\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}+\frac{z^2-y^2}{x+y}\ge0\)
xD
Có: \(\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}+\frac{z^2-y^2}{x+y}\)(1)
\(=\frac{\left(x-z\right)\left(x+z\right)}{y+z}+\frac{\left(y-x\right)\left(x+y\right)}{z+x}+\frac{\left(z-y\right)\left(y+z\right)}{x+y}\)
\(\left(1\right)=S_1\left(x-z\right)^2+S_2\left(y-x\right)^2+S_3\left(z-y\right)^2\)
Trong đó:
\(\hept{\begin{cases}S_1=\frac{x+z}{\left(y+z\right)\left(x-z\right)}\\S_2=\frac{x+y}{\left(z+x\right)\left(y-x\right)}\\S_3=\frac{y+z}{\left(x+y\right)\left(z-y\right)}\end{cases}}\)
Giả sử: \(x\ge y\ge z\)( x,y,z lớn hơn 0)
Có: \(S_1=\frac{x+z}{\left(y+z\right)\left(x-z\right)}\ge0\)
Xét: \(S_1+S_2=\frac{x+z}{\left(y+z\right)\left(x-z\right)}-\frac{x+y}{\left(x+z\right)\left(x-y\right)}=\frac{\left(x+z\right)^2+\left(x+y\right)\left(y+z\right)^2+\left(y+z\right)\left(y-z\right)\left(2x+y+z\right)}{.....}\ge0\)
Xét tiếp \(S_1+S_3\)là xong
Không biết đúng k tại mình hơi yếu
*Nếu được giả sử như bạn Cà Bùi thì bài làm của em như sau,mong mọi người góp ý ạ!
Ta có: \(VT=\frac{x^2-z^2}{y+z}+\frac{y^2-x^2}{z+x}-\frac{x^2-z^2+y^2-x^2}{x+y}\)
\(=\left(x^2-z^2\right)\left(\frac{x+y-y-z}{\left(x+y\right)\left(y+z\right)}\right)+\left(y^2-x^2\right)\left(\frac{x+y-z-x}{\left(z+x\right)\left(x+y\right)}\right)\) (nhóm các số thích hợp + quy đồng)
\(=\frac{\left(x+z\right)\left(x-z\right)^2}{\left(x+y\right)\left(y+z\right)}+\frac{\left(y-x\right)\left(y-z\right)}{\left(z+x\right)}\)
Do a, b, c có tính chất hoán vị, nên ta giả sử y là số lớn nhất. Khi đó vế trái không âm hay ta có đpcm.
Cho góc lượng giác ( OA; OB) có số đo bằng π/5. Hỏi trong các số sau, số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác ( OA; O B) ?
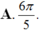
![]()
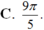
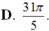
1. Biết rằng một tam giác có cả ba góc bằng nhau
- Hãy cho biết số đo các góc của tam giác đó
- Hãy cho biết số đo các góc ngoài của tam giác đó.

2. Xem hình trên. Với hình 1, tam giác đã cho là một tam giác vuông, có một góc nhọ là x và góc nhọn kia là 50o suy ra: x + 50o = 90o hay x = 40o
cho biết số đo các góc y, z, t, m trong mỗi hình vẽ ở hình trên
1. Biết rằng một tam giác có cả ba góc bằng nhau
- Hãy cho biết số đo các góc của tam giác đó
- Hãy cho biết số đo các góc ngoài của tam giác đó.
2. Xem hình trên. Với hình 1, tam giác đã cho là một tam giác vuông, có một góc nhọ là x và góc nhọn kia là 50o suy ra: x + 50o = 90o hay x = 40o
cho biết số đo các góc y, z, t, m trong mỗi hình vẽ ở hình trên
bài 1:
a) Gọi số đo các góc của tam giác trên là x; y; z; ta có:
x = y = z theo đề bài
x + y + z = 180 độ (tổng 3 góc trong tam giác)
=> x + x + x = 180 độ
x = 60 độ
vậy số đo 3 góc của tam giác trên cùng bằng 60 độ
b) số đo các góc ngoài của tam giác trên cùng bằng 180 độ - 60 độ = 120 độ