Phương trình x3 + 2x2 + (m + 1)x + 2(m + 1) = 0 có ba nghiệm lập thành cấp số nhân.
A. -1; -3; -4
B. -1; 13; -4
C. 1; 3; 4
D. không có giá trị nào thoả mãn
Tìm m để phương trình x 3 − 3 x 2 − 9 x + m = 0 (1) có ba nghiệm phân biệt lập thành cấp số cộng.
A. m = 10
B. m = 11
C. m = 12
D. m = 9
Đáp án A
Điều kiện cần: Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng, khi đó
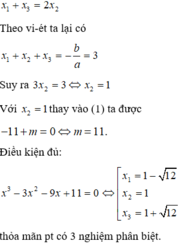
Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: x3 – 7mx2 + 2(m2 + 6m)x – 64 = 0.
A. m = 8
B. m = 0
C. m = -1hoặc m = 7
D. m = 0 hoặc m = 8
Chọn A.
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x1; x2; x3 lập thành một cấp số nhân.
Theo định lý Vi-ét, ta có x1.x2.x3 = 64
Theo tính chất của cấp số nhân, ta có x1x3 = x22. Suy ra ta có x23 = 64 ⇔ x2 = 4
Thay x = 4 vào phương trình đã cho ta được: 43 – 7m.42 + 2(m2 + 6m).4 – 64 = 0
⇔ m2 – 8m = 0
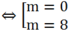
+ Điều kiện đủ: Với m = 0 thay vào phương trình đã cho ta được: x3 – 64 = 0 hay x = 4
(nghiệm kép-loại)
Với m = 8 thay vào phương trình đã cho nên ta có phương trình x3 – 56x2 + 224x – 64 = 0
Giải phương trình này, ta được 3 nghiệm phân biệt lập thành cấp số nhân.
Vậy m = 8 là giá trị cần tìm.
Tìm m để phương trình: x 3 − 3 x 2 + mx + 2 − m = 0 có 3 nghiệm phân biệt lập thành 1 cấp số cộng:
A. m ∈ − 3 ; + ∞ .
B. m ∈ ℝ .
C. m = 3
D. m ∈ − ∞ ; 3 .
Đáp án D
· Điều kiện cần:
Giả sử phương trình đã cho có 3 nghiệm phân biệt x 1 ; x 2 ; x 3 lập thành một cấp số cộng
Khi đó: x 1 + x 3 = 2 x 2 x 1 + x 2 + x 3 = 3 ⇔ 3 x 2 = 3 ⇔ x 2 = 1 .
Với x 2 = 1 thay vào phương trình ta được:
1 − 3 + m + 2 − m = 0 (luôn đúng).
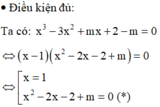
Phương trình đã cho có 3 nghiệm phân biệt tương đương với phương trình (*) có 2 nghiệm phân biệt khác 1.
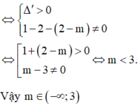
Tìm m để phương trình x 3 − 3 x 2 − 9 x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.
A. m = 16
B. m= 11
C. m= 13
D. m = 12
Chọn B.
Điều cần cần:
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
Khi đó: x 1 + x 3 = 2 x 2 ,
Lại có :
x 1 + x 2 + x 3 = − b a = 3 ⇒ x 2 = 1
Thay vào phương trình ta được: 13 – 3.12 – 9.1 + m =0
⇔ m = 11
* Điều kiện đủ : Với m =11 phương trình trở thành :
x 3 − 3 x 2 − 9 x + 11 = 0
⇔ x − 1 x 2 − 2 x − 11 = 0 ⇔ x 1 = 1 − 12 , x 2 = 1, x 3 = 1 + 12
Ba nghiệm này lập thành cấp số cộng.
Vậy m =11 là giá trị cần tìm.
Tìm tất cả các giá trị của tham số m để phương trình sau có ba nghiệm phân biệt lập thành một cấp số nhân: x 3 − 7 x 2 + 2 m 2 + 6 m x − 8 = 0.
A. m = -7
B. m= 1
C. m = -1 hoặc m= 7
D. m = 1 hoặc m = -7
Chọn D
+ Điều kiện cần: Giả sử phương trình đã cho có ba nghiệm phân biệt x 1 , x 2 , x 3 lập thành một cấp số nhân.
Theo định lý Vi-ét, ta có x 1 . x 2 . x 3 = 8
Theo tính chất của cấp số nhân, ta có x 1 x 3 = x 2 2 . Suy ra ta có x 2 3 = 8 ⇔ x 2 = 2.
Với nghiệm x=2, ta có m 2 + 6 m − 7 = 0 ⇔ m = 1 m = − 7
+ Điều kiện đủ: Với m= 1 hoặc m = -7 thì m 2 + 6 m = 7 nên ta có phương trình: x 3 − 7 x 2 + 14 x − 8 = 0.
Giải phương trình này, ta được các nghiệm là 1,2,4 Hiển nhiên ba nghiệm này lập thành một cấp số nhân với công bôị q=2
Vậy m= 1 và m= -7 là các giá trị cần tìm.
Xác định m để: Phương trình x3 – 3x2 – 9x + m = 0 có ba nghiệm phân biệt lập thành cấp số cộng.
A. m = 16
B. m = 11
C. m = 13
D. m = 12
Chọn B.
Giải sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
Khi đó: x1 + x3 = 2x2, x1 + x2 + x3 = 3 ⇒ x2 = 1
Thay vào phương trình ta có m = 11.
Với m = 11 ta có phương trình : x3 – 3x2 – 9x + 11 = 0
⇔ (x – 1)(x2 – 2x – 11) = 0 ⇔ ![]()
Ba nghiệm này lập thành CSC.
Vậy m = 11 là giá trị cần tìm.
Bài 1: Tìm m để phương trình sau có 3 nghiệm lập thành 1 cấp số cộng:
1, \(x^3-x^2-m^2x+m^2=0\)
2, \((x-2)(x^2-2mx+2m+3)=0\)
3, \(x^3-(2m-3)x^2-mx+m-2=0\)
4, \(x^3+(2m-1)x^2+(4m+1)x+2m+3=0\)
Bài 2: Tìm m để phương trình sau có 4 nghiệm lập thành 1 cấp số cộng:
a, \(-x^4+2mx^2-2m+1=0\)
b, \(x^4+2(m-2)x^2+m^2-5m+5=0\)
Bài 3: Tìm 3 số lập thành 1 cấp số cộng biết tổng của chúng bằng tổng các bình phương bằng 83
Giá trị của m để phương trình có ba nghiệm phân biệt lập thành một cấp số cộng x 3 - 3 x 2 + x - m = 0 thuộc khoảng nào trong các khoảng dưới đây?
A.(2;4)
B.(-2;0)
C.(0;2)
D.(-4;2)
Giá trị của m để phương trình x 3 - 3 x 2 + x - m = 0 có ba nghiệm phân biệt lập thành một cấp số cộng thuộc khoảng nào trong các khoảng dưới đây?
A. (2;4).
B. (-2;0).
C. (0;2).
D. (-4;2).
Chọn B.
Xét hàm số f(x) =
x
3
-
3
x
2
+
x
-
m
, ![]()
![]()
Điểm uốn của đồ thị hàm số là A (1;-1-m).
Phương trình x 3 - 3 x 2 + x - m = 0 có ba nghiệm phân biệt lập thành một cấp số cộng.
![]()