Cho hàm số f ( x ) = tan x x ; x k h á c 0 ∧ x k h á c π 2 + k π ; k ∈ ℤ 0 ; x = 0 Hàm số y = f(x) liên tục trên các khoảng nào sau đây?
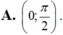
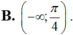
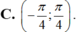
![]()
Cho y = x cos 2 x trên - π 2 ; π 2 và F(x) là một nguyên hàm của hàm số xf ‘(x) thỏa mãn F(0) = 0. Biết a ∈ - π 2 ; π 2 thỏa mãn tan a = 3. Tính F(a) – 10a2 + 3a
A. 1 2 ln 10
B. - 1 4 ln 10
C. - 1 2 ln 10
D. ln 10
Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
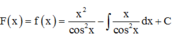
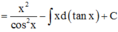
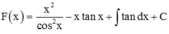
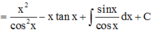

![]()
![]()
=> 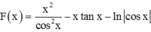
![]()
![]()
![]()
![]()
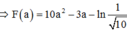
![]()
![]()
Trong các hàm số sau, hàm số nào là nguyên hàm của hàm số f(x)= tan2x ?
ĐÁP án là D \(\int\left(tan\left(x\right)^2\right)=\int\left(\frac{1}{cos\left(x\right)^2}-1\right)=-x+tan\left(x\right)\)
Trong các hàm số sau, hàm số nào là nguyên hàm của hàm số f(x)= tan2x ?
Cho hàm số f(x) = cos 2x và g(x) = tan 3x, chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm số lẻ
B. f(x)là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x)là hàm số lẻ, g(x) là hàm số chẵn
D. f(x) và g(x) đều là hàm số lẻ.
Cho hàm số f x = tan x 2 c o t x + 2 cos x + 2 cos 2 x có
nguyên hàm là F(x) và F π 4 = π 2 .
Giả sử F x = a x + b cos x - cos c x 2 - d .Chọn phát biểu
đúng:
A. a : b : c = 1 : 2 : 1
B. a + b + c = 6
C. a + b = 3c
D. a – b + c = d
Tính đạo hàm của hàm số \(f\left( x \right) = \tan x\) tại điểm \({x_0} = - \frac{\pi }{6}\)
\(f'\left( x \right) = \frac{1}{{{{\cos }^2}x}} \Rightarrow f'\left( { - \frac{\pi }{6}} \right) = \frac{1}{{{{\cos }^2}\left( { - \frac{\pi }{6}} \right)}} = \frac{4}{3}\)
Cho hàm số \(f\left(x\right)=\dfrac{x+1}{x^2+x-6}\) và \(g\left(x\right)=\tan x+\sin x\)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục ?
+) Hàm số  xác định khi và chỉ khi x2+ x – 6 ≠ 0 <=> x ≠ -3 và x ≠ 2.
xác định khi và chỉ khi x2+ x – 6 ≠ 0 <=> x ≠ -3 và x ≠ 2.
Hàm số f(x) liên tục trên các khoảng (-∞; -3), (-3; 2) và (2; +∞)
+) Hàm số g(x) = tanx + sinx xác định khi và chỉ khi
tanx ≠ 0 <=> x ≠ π/2 +kπ với k ∈ Z.
Hàm số g(x) liên tục trên các khoảng ( – π/2+kπ; π/2 +kπ) với k ∈ Z.
Cho hàm số f(x) liên tục trên R và các tích phân ∫ 0 π 4 f ( tan x ) d x = 4 và ∫ 0 1 x 2 f ( x ) x 2 + 1 d x , tính tích phân I = ∫ 0 1 f ( x ) d x
A. 6
B. 2
C. 3
D. 1
Chọn A.
Đặt t = tan x => dt = (1+ tan x) dx => d t 1 + t 2 = d x
Đổi cận x = 0=> t = 0 và x = π 4 = > t = 1
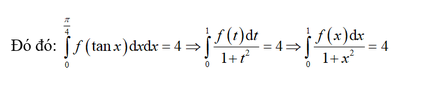
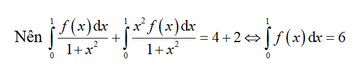
Tìm họ nguyên hàm của hàm số :
\(f\left(x\right)=\frac{\sin3x\sin4x}{\tan x+\cot2x}\)
Ta biến đổi :
\(f\left(x\right)=\frac{\sin3x\sin4x}{\tan x+\cot2x}=\frac{\sin3x\sin4x}{\frac{\sin x.\sin2x+\cos x.\cos2x}{\cos x.\sin2x}}=\frac{\sin3x\sin4x}{\frac{\cos x}{\cos x.\sin2x}}=\sin3x\sin4x\sin2x\)
\(=\frac{1}{2}\left(\cos x-\cos7x\right)\sin2x=\frac{1}{2}\left[\sin2x\cos x-\cos7x\sin2x\right]=\frac{1}{4}\left(\sin3x+\sin x-\sin9x+\sin5x\right)\)
Do đó :
\(I=\int\left(\frac{1}{4}\left(\sin3x+\sin x-\sin9x+\sin5x\right)\right)dx=-\frac{1}{2}\cos3x-\frac{1}{4}\cos x+\frac{1}{9}\cos9x-\frac{1}{5}\cos5x+C\)