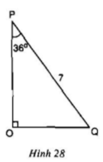
Ta có: ∠P + ∠Q = 90o ⇒ ∠ Q = 90o - 36o= 54o

Xét tam giác OPQ vuông tại O

OP = PQ.cosP = 7.cos 36o ≈ 5,66

OQ = PQ.cosQ = 7.cos 54o ≈ 4,11

HS tự chứng minh 

Định lí:

Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng.

Ta có các hệ thức sau: a² = b² + c² - 2bc.cosA (1)

b² = a² + c² - 2bc.cosB (2)

c² = a² + b² - 2bc.cosC (3)

Hệ quả: Từ định lí cosin suy ra:

cosA = cosB =

cosC =

Gửi vào zalo r nhá

MQ = 4cm

Biết M là trung điểm của OP thì \(OM=MP=\frac{OP}{2}\) hay \(OM=MP=\frac{4}{2}=2\left(\text{cm}\right)\)

\(\Rightarrow MP=2\text{cm}\)

Vì N là trung điểm của OQ nên ta có:

\(OP+PQ=OQ\)

hay \(4+PQ=6\)

\(PQ=6-4\)

\(PQ=2\left(\text{cm}\right)\)

Mà \(MP+PQ=MQ\) nên ta có:

\(MP+PQ=MQ\)

hay \(2+2=MQ\)

\(MQ=4\left(\text{cm}\right)\)

Vậy \(MQ\)dài \(4\text{cm}.\)

Ta có hình vẽ:

a) Vì \(OP\perp OM\Rightarrow POM=90^o;OQ\perp ON\Rightarrow QON=90^o\)

Ta có: MOP + PON = MON

=> 90^o + PON = 140^o

=> PON = 140^o - 90^o = 50^o (1)

Lại có: MOQ + QON = MON

=> MOQ + 90^o = 140^o

=> MOQ = 140^o - 90^o = 50^o (2)

Từ (1) và (2) => PON = MOQ = 50^o

b) Ta có: POQ + PON = QON

=> POQ + 50^o = 90^o

=> POQ = 90^o - 50^o = 40^o

Giải:

Ta có: \(\widehat{MOQ}+\widehat{NOQ}=\widehat{MON}\)

\(\Rightarrow\widehat{MOQ}+90^o=140^o\) ( vì OQ _|_ ON nên \(\widehat{NOQ}=90^o\) )

\(\Rightarrow\widehat{MOQ}=50^o\)

\(\widehat{MOP}+\widehat{NOP}=\widehat{MON}\)

\(\Rightarrow90^o+\widehat{NOP}=140^o\) ( vì OP _|_ OM nên \(\widehat{MOP}=90^o\) )

\(\Rightarrow\widehat{NOP}=50^o\)

\(\Rightarrow\widehat{MOQ}=\widehat{NOP}=50^o\)

b) Ta có: \(\widehat{MOQ}+\widehat{POQ}+\widehat{NOP}=\widehat{MON}\)

\(\Rightarrow50^o+\widehat{POQ}+50^o=120^o\)

\(\Rightarrow\widehat{POQ}=20^o\)

Bạn tự vẽ hình nha

a.

MOQ + QON  = MON

MOQ + 90⁰ = 140⁰

MOQ = 140⁰ - 90⁰

MOQ = 50⁰

NOP + POM = MON

NOP + 90⁰ = 140⁰

NOP = 140⁰ - 90⁰

NOP = 50⁰

mà MOQ = 50⁰

=> NOP = MOQ

b.

MOQ + QOP + PON = MON

50⁰ + QOP + 50⁰ = 140⁰

QOP = 140⁰ - 50⁰ - 50⁰

QOP = 40⁰

Chúc bạn học tốt

a)Vì OP vuông góc với OM, OQ vuông góc với ON

         Suy ra:MOP=QON=90⁰

Mà MOQ+POQ=90⁰(1)

      NOP+POQ=90⁰(2)

  Từ (1) và (2) suy ra MOQ=NOP

b)     Vì MON=MOP+PON

Thay số:140⁰=90⁰+PON

              PON=140⁰-90⁰=50⁰

Mà PON=MOQ

Tacó:MON=MOQ+PON+QOP

Thay số:140⁰=50⁰+50⁰+POQ

               POQ=40⁰

hình đâu pn

Câu a phải là so sánh mOQ và nOP chứ bạn?!

a, Do OP vuông góc với OM=> góc mOp = 90^0

Do OQ vuông góc với ON => góc nOq = 90^0

=> góc mOp = góc nOq

b,Ta có nOp = góc mOn - góc mOp = 140^0 - 90^0 = 30^0

Vậy góc pOq = góc nOq - góc nOp = 90^0 -30^0 = 60^0

a)Ta có:

\(\widehat{mOP}+\widehat{nOP}=\widehat{mOn}\)(tia OP nằm giữa 2 tia Om và On)

\(\Rightarrow90^o+\widehat{nOP}=140^o\)

\(\Rightarrow\widehat{nOP}=140^o-90^o\)

\(\Rightarrow\widehat{nOP}=50^o\left(1\right)\)

Ta lại có:\(\widehat{nOQ}+\widehat{nOQ}=\widehat{mOn}\)(tia OQ nằm giữa 2 tia Om và On)         

\(\Rightarrow90^o+\widehat{nOQ}=140^o\)

\(\Rightarrow\widehat{nOQ}=140^o-90^o\)

\(\Rightarrow\widehat{nOQ}=50^o\left(2\right)\)

Từ (1) và (2), suy ra:\(\widehat{mOQ}=\widehat{nOP}\left(đpcm\right)\)

b)Ta có:\(\widehat{mOQ}+\widehat{POQ}+\widehat{nOP}=\widehat{mOn}\)

\(\Rightarrow50^o+\widehat{POQ}+50^o=140^o\)

\(\Rightarrow100^o+\widehat{POQ}=140^o\)

\(\Rightarrow\widehat{POQ}=140^o-100^o\)

Vậy\(\widehat{POQ}=40^o\)