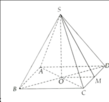
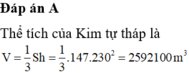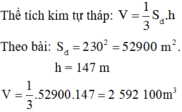Có một hình kim tự tháp có cạnh đáy là 5cm tính thể tích hình đó.

Những câu hỏi liên quan
Một kim tự tháp được xây dựng dạng hình chóp có đáy là hình vuông và các mặt bên là các tam giác cân biết cạnh bên và cạnh đáy của hình chóp lần lượt là 120m và 140m. thể tích của hình chóp được tính theo công thức S=1/3S.h trong đó S là diện tích đáy, h là chiều cao hình chóp. Tính chiều cao và thể tích của kim tự tháp trên.
Kim tự tháp Kê-ôp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231m. Tính diện tích xung quanh và thể tích của kim tự tháp
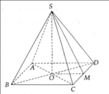
Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.
Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.
Tính được:
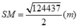
Diện tích xung quanh của kim tự tháp là:
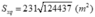
Thể tích của kim tự tháp:
V = 2436819 (m3)
Đúng 0
Bình luận (0)
Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.
1. **Tính cạnh bên**:
Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.
Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:
\[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]
\[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]
\[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]
2. **Tính diện tích một mặt bên**:
Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:
\[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]
Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:
\[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]
\[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]
\[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]
Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).
Đúng 0
Bình luận (0)
Bảo tàng Louvre (Pháp) có một kim tự tháp hình chóp tứ giác đều bằng kính (gọi là kim tự tháp Louvre) có chiều cao \(21,3\)m và cạnh đáy \(34\)m. Tính thể tích của kim tự tháp này.

Thể tích của kim tự tháp là: \(\frac{1}{3}{.34^2}.21,3 = 8207,6\) (\({m^3}\))
Đúng 0
Bình luận (0)
Kim tự tháp Kê-ốp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231 m. Tính cạnh bên và diện tích một mặt bên của kim tự tháp.
Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này có hình dạng là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Tính thể tích của Kim tự tháp
Đọc tiếp
Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này có hình dạng là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Tính thể tích của Kim tự tháp
![]()
![]()
![]()
![]()
Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này có hình dạng là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Tính thể tích của Kim tự tháp A. 2592100
m
3
B. 2592009
m
3
C. 7776300
m
3
D. 3888150
m
3
Đọc tiếp
Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này có hình dạng là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Tính thể tích của Kim tự tháp
A. 2592100 m 3
B. 2592009 m 3
C. 7776300 m 3
D. 3888150 m 3
Đáp án A
Thể tích của Kim tự tháp là V = 1 3 S h = 1 3 .147.230 2 = 2592100 m 3
Đúng 0
Bình luận (0)
Xét các hình sau:Kim tự tháp Lu-vrơ: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-Vrơ. Mô hình có dạng hình chóp đều cao 21m, độ dài cạnh đáy là 34m.a. Cạnh bên hình chóp là bao nhiêu?b. Tính thể tích hình chópc. Tính tổng diện tích các tẩm kính để phủ lên hình chóp này
Đọc tiếp
Xét các hình sau:
Kim tự tháp Lu-vrơ: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-Vrơ. Mô hình có dạng hình chóp đều cao 21m, độ dài cạnh đáy là 34m.
a. Cạnh bên hình chóp là bao nhiêu?
b. Tính thể tích hình chóp
c. Tính tổng diện tích các tẩm kính để phủ lên hình chóp này
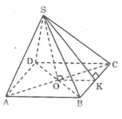
Tương tự câu 1, trong đó tổng diện tích các tấm kính để phủ lên hình chóp chính là diện tích xung quanh của hình chóp
Đúng 0
Bình luận (0)
Kim tự tháp Kheops - Ai Cập có dạng hình mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m
a) Tính chiều cao h của kim tự tháp ( làm tròn đến mét)
b) Cho biết thể tích của hình chóp được tính theo công thức V 1/3S.h, trong đó S là diện tích mặt đáy, h là chiều cao hình chóp. Tính theo m3 thể tích của kim tự tháp này (làm tròn đến hàng nghìn)
Đọc tiếp
Kim tự tháp Kheops - Ai Cập có dạng hình mặt bên là các tam giác cân chung đỉnh (hình vẽ). Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m
a) Tính chiều cao h của kim tự tháp ( làm tròn đến mét)
b) Cho biết thể tích của hình chóp được tính theo công thức V = 1/3S.h, trong đó S là diện tích mặt đáy, h là chiều cao hình chóp. Tính theo m3 thể tích của kim tự tháp này (làm tròn đến hàng nghìn)
Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước công nguyên. Kim tự tháp này là một hình chóp tứ giác đều có chiều cao là 147m, cạnh đáy dài 230m. Tính thể tích của nó. A. 2 592 100m3 B. 52900 m3 C. 7776300 m3 D. 1470000 m3
Đọc tiếp
Kim tự tháp Kê-ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước công nguyên. Kim tự tháp này là một hình chóp tứ giác đều có chiều cao là 147m, cạnh đáy dài 230m. Tính thể tích của nó.

A. 2 592 100m3
B. 52900 m3
C. 7776300 m3
D. 1470000 m3