Số gia của hàm số f(x)= x 2 2 ứng với số gia ∆ x của đối số x tại x 0 = - 1 là
A. 1 2 ∆ x 2 - ∆ x
B. 1 2 ( ∆ x ) 2 - ∆ x
C. 1 2 ( ∆ x ) 2 + ∆ x
D. 1 2 ( ∆ x ) 2 + ∆ x
Những câu hỏi liên quan
số gia của hàm số y = f(x) = \(\dfrac{^{x^3}}{2}\) ứng với số gia △t của đối số tại x\(_0\) = -1 là :
Số gia của hàm \(f\left(x\right)\) phải ứng với số gia \(\Delta x\) của đối số chứ sao lại \(\Delta t\), em kiểm tra lại đề bài
Đúng 0
Bình luận (0)
Cho hàm số f(x)
x
2
-
x
, đạo hàm của hàm số ứng với số gia của đối số x tại
x
0
là A.
lim
∆
x
→
0
∆
x
2
+
2...
Đọc tiếp
Cho hàm số f(x) = x 2 - x , đạo hàm của hàm số ứng với số gia của đối số x tại x 0 là
A. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x - ∆ x
B. lim Δ x → 0 ( Δ x + 2 x − 1 )
C. lim ∆ x → 0 ∆ x + 2 x + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x + ∆ x
Số gia của hàm số
f
(
x
)
x
2
ứng với số gia δx của đối số x tại
x
0
-
1
là A.
∆
x
2
-
2
∆
x
-
1
B.
∆
x
2
+
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 ứng với số gia δx của đối số x tại x 0 = - 1 là
A. ∆ x 2 - 2 ∆ x - 1
B. ∆ x 2 + 2 ∆ x + 2
C. ∆ x 2 + 2 ∆ x
D. ∆ x 2 - 2 ∆ x
- Với số gia của đối số x tại điểm x 0 = - 1 , ta có:
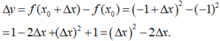
Chọn D.
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
2
−
x
, đạo hàm của hàm số ứng với số gia
Δ
x
của đối số x tại
x
0
là A.
lim
Δ
x
→
0
Δ
x
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 − x , đạo hàm của hàm số ứng với số gia Δ x của đối số x tại x 0 là
A. lim Δ x → 0 Δ x 2 + 2 x Δ x − Δ x .
B. lim Δ x → 0 Δ x + 2 x − 1 .
C. lim Δ x → 0 Δ x + 2 x + 1 .
D. lim Δ x → 0 Δ x 2 + 2 x Δ x + Δ x .
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là A.
lim
∆
x
→
0
∆
x
2
+
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là
A. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x - 1
C. lim ∆ x → 0 ∆ x + 2 x + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x + ∆ x
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là: A.
lim
∆
x
→
0
∆
x
2
-
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là:
A. lim ∆ x → 0 ∆ x 2 - 2 x 0 ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x 0 - 1
C. lim ∆ x → 0 ∆ x + 2 x 0 + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x 0 ∆ x + ∆ x
Cho hàm số
f
(
x
)
x
2
−
x
, đạo hàm của hàm số ứng với số gia
Δ
x
của đối số x tại x0 là A.
lim
Δ
x
→
0
Δ
x
2
+...
Đọc tiếp
Cho hàm số f ( x ) = x 2 − x , đạo hàm của hàm số ứng với số gia Δ x của đối số x tại x0 là
A. lim Δ x → 0 Δ x 2 + 2 x Δ x − Δ x .
B. lim Δ x → 0 Δ x + 2 x − 1 .
C. lim Δ x → 0 Δ x + 2 x + 1 .
D. lim Δ x → 0 Δ x 2 + 2 x Δ x + Δ x .
Đáp án B
Ta có
Δ y = ( x 0 + Δ x ) 2 − ( x 0 + Δ x ) − ( x 0 2 − x 0 ) = △ x 2 + 2 x 0 Δ x − Δ x .
Nên
f ' ( x 0 ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 ( Δ x ) 2 + 2 x 0 Δ x − Δ x Δ x = lim Δ x → 0 ( Δ x + 2 x 0 − 1 ) .
Vậy f ' ( x ) = lim Δ x → 0 ( Δ x + 2 x − 1 ) .
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
x
2
+
2
x
,có ∆x là số gia của đối số tại x1, ∆y là số gia tương ứng của hàm số. Khi đó ∆y bằng: A.
(
∆
x
)
2
+
2
∆
x
B.
(
∆
x
)...
Đọc tiếp
Cho hàm số f ( x ) = x 2 + 2 x ,có ∆x là số gia của đối số tại x=1, ∆y là số gia tương ứng của hàm số. Khi đó ∆y bằng:
A. ( ∆ x ) 2 + 2 ∆ x
B. ( ∆ x ) 2 + 4 ∆ x
C. ( ∆ x ) 2 + 2 ∆ x - 3
D. 3
∆y=f(1+∆x)-f(1)=(1+∆x)2+2(1+∆x)-(1+2)=(∆x)2+4∆x
Đáp án B
Chú ý. Tránh các sai lầm thay trực tiếp ∆x hoặc 1 vào hàm (A,D) hoặc lấy hiệu của f(∆x) và f(1) (C)
Đúng 0
Bình luận (0)
Số gia của hàm số
f
(
x
)
x
2
2
ứng với số gia Δx của biến số x tại
x
0
-
1
là A.
1
2
∆
x
2
-
∆
x
B.
1
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 2 ứng với số gia Δx của biến số x tại x 0 = - 1 là
A. 1 2 ∆ x 2 - ∆ x
B. 1 2 ∆ x 2 - ∆ x
C. 1 2 ∆ x 2 + ∆ x
D. 1 2 ∆ x 2 + ∆ x
- Với số gia Δx của biến số x tại x 0 = - 1 . Ta có:
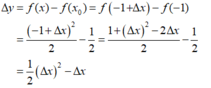
Chọn A.
Đúng 0
Bình luận (0)