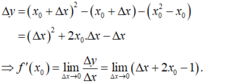Các câu hỏi tương tự
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là A.
lim
∆
x
→
0
∆
x
2
+
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là
A. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x - 1
C. lim ∆ x → 0 ∆ x + 2 x + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x + ∆ x
Cho hàm số
y
f
x
a
x
5
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 5 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 . Biết f'(-1)=3 . Tính lim ∆ x → 0 f 1 + ∆ x - f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Vi phân của hàm số f(x) = sin(3x – 2) + cos(x2 + 1) tại điểm x = 0 ứng với Δx = 0,5 xấp xỉ bằng:
A: -0,24
B: -0,624
C: -0,364
D: Đáp án khác
tính giới hạn của hàm số
lim x->0 : \(\frac{\left(\sqrt{1+x^2}+x\right)^n-\left(\sqrt{1+x^2}-x\right)^n}{x^2}\)
Cho hàm số
f
(
x
)
x
2
sin
1
x
n
ế
u
x
...
Đọc tiếp
Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?
1) đạo hàm của hàm số \(\dfrac{2x^2+1}{x^2}\) là
2) cho hàm số \(f\left(x\right)=\sqrt{-5x^2+14x-9}\) tập hợp các giá trị của x để f'(x) = 0 là
cho hàm số yfleft(xright) liên tục trên R thỏa limlimits_{xrightarrow-infty}fleft(xright)+infty , limlimits_{xrightarrow+infty}fleft(xright)-dfrac{1}{2}tìm số đường tiệm cận củ đồ thị hàm số đã cholimlimits_{xrightarrow-infty}fleft(xright)+infty
Đọc tiếp
cho hàm số \(y=f\left(x\right)\) liên tục trên R thỏa
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\) , \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=-\dfrac{1}{2}\)
tìm số đường tiệm cận củ đồ thị hàm số đã cho
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=+\infty\)
Số gia của hàm số
f
(
x
)
x
2
ứng với số gia δx của đối số x tại
x
0
-
1
là A.
∆
x
2
-
2
∆
x
-
1
B.
∆
x
2
+
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 ứng với số gia δx của đối số x tại x 0 = - 1 là
A. ∆ x 2 - 2 ∆ x - 1
B. ∆ x 2 + 2 ∆ x + 2
C. ∆ x 2 + 2 ∆ x
D. ∆ x 2 - 2 ∆ x
Cho hàm số
f
(
x
)
3
-
4
-
x
4
k
h
i
x...
Đọc tiếp
Cho hàm số f ( x ) = 3 - 4 - x 4 k h i x ≢ 0 1 4 k h i x = 0 . Khi đó đạo hàm của hàm số tại điểm x = 0 là kết quả nào sau đây?
A. 1 4
B. 1 16
C. 1 32
D. Không tồn tại