Cho hàm số f ( x ) = l n ( e x + m ) . Có bao nhiêu số thực dương m để f ' a + f ' b = 1 với mọi số thực a,b thỏa mãn a+b=1
A. 1
B. 2
C. Vô số
D. 0
Cho hàm số f ( x ) = ln e x + m Có bao nhiêu số thực dương m để f'(a) + f'(b)=1 với mọi số thực a, b thỏa mãn a + b = 1
A. 1
B. 2
C. Vô số
D. 0
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e có bảng biến thiên như hình vẽ sau
Có bao nhiêu số nguyên dương m để hàm số y=|f(x)+m| có 7 điểm cực trị.
A. 0.
B. 21.
C. 18.
D. 19.
Cho hàm số f ( x ) = e x 2 + 1 ( e x - e - x ) Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình f ( m - 7 ) + f ( 12 m + 1 ) ≤ 0
A. 4
B. 6.
C. 3.
D. 5.
Cho hàm số \(f\left(x\right)=e^{\sqrt{x^2+1}}\left(e^x-e^{-x}\right)\). Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình \(f\left(m-7\right)+f\left(\dfrac{12}{m+1}\right)< 0\) ?
Lời giải:
Đặt $\sqrt{x^2+1}+x=a$ thì:
$f(a)=e^a-e^{\frac{1}{a}}$
$f'(a)=e^a+\frac{1}{a^2}.e^{\frac{1}{a}}>0$ với mọi $a$
Do đó hàm $f(a)$ là hàm đồng biến hay $f(x)$ là hàm đồng biến trên R
$\Rightarrow f(x)> f(0)=0$ với mọi $x>0$
$\Rightarrow f(\frac{12}{m+1})>0$ với $m$ nguyên dương
Do đó để $f(m-7)+f(\frac{12}{m+1})<0$ thì $f(m-7)<0$
$\Rightarrow m-7<0$
Mặt khác, dễ thấy: $f(x)+f(-x)=0$. Bây h xét:
$m=1$ thì $f(m-7)+f(\frac{12}{m+1})=f(-6)+f(6)=0$ (loại)
$m=2$ thì $f(m-7)+f(\frac{12}{m+1})=f(-5)+f(4)=f(4)-f(5)<0$ (chọn)
$m=3$ thì $f(m-7)+f(\frac{12}{m+1})=f(-4)+f(3)=f(3)-f(4)<0$ (chọn)
$m=4$ thì $f(m-7)+f(\frac{12}{m+1})=f(-3)+f(2,4)=f(2,4)-f(3)<0$ (chọn)
$m=5$ thì $f(m-7)+f(\frac{12}{m+1})=f(-2)+f(2)=0$ (loại)
$m=6$ thì $f(m-7)+f(\frac{12}{m+1})=f(-1)+f(12/7)>f(-1)+f(1)=0$ (loại)
Vậy có 3 số tm
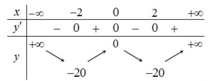
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
Có bao nhiêu số nguyên dương m để phương trình f(2 sinx+1)=f(m) có nghiệm thực ?
A. 2.
B. 5.
C. 4.
D. 3.
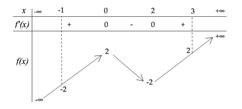
Cho hàm số f ( x ) = m - 2 x 3 - 2 2 m - 3 x 2 + 5 m - 3 x - 2 m - 2 với m là tham số thực. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x có 5 điểm cực trị?
A. 0.
B. 3.
C. 2.
D. 1.
Hàm số y = f x với f(x) là hàm đa thức bậc 3 có 5 điểm cực trị khi và chỉ khi hàm số f(x) có hai cực trị và đồ thị của hàm số cắt trục hoành tại 3 điểm phân biệt.
Mặt khác, f(x) là hàm số bậc 3 nên khi đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt thì hàm số đồng thời cũng có hai cực trị. Do đó ta chỉ cần tìm điều kiện để phương trình f(x) = 0 có 3 nghiệm phân biệt.

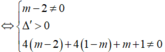
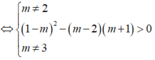
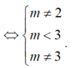

Chọn D
Cho hàm số f ( x ) = ln x + x 2 + 1 Với mỗi số nguyên dương m đặt S m = f ( - m ) + f ( - m + 1 ) + . . + ( 0 ) + . . + f ( m - 1 ) Có bao nhiêu giá trị của m để phương trình 8 x - 3 . 4 x - S m = 0 có hai nghiệm thực phân biệt
A. 27
B. 2
C. 28
D. 1
Đặt
t
=
2
x
(
t
>
0
)
phương trình trở thành: ![]()
Xét hàm số ![]() trên khoảng
0
;
+
∞
có
trên khoảng
0
;
+
∞
có
![]()
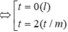
Bảng biến thiên:
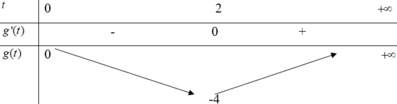
Với mỗi t > 0 cho một nghiệm duy nhất
x
=
log
2
t
Vậy phương trình có hai nghiệm thực phân biệt khi và chỉ khi (∗) có hai nghiệm phân biệt t > 0. Quan sát bảng biến thiên suy ra ![]()
Ta đi rút gọn Sm: Có
![]()
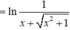
![]()
Do đó ![]() Vì vậy
Vì vậy
![]()
![]()
![]()
![]()
![]()
Vậy điều kiện là
![]()
![]()
![]()
![]()
Có tất cả 27 số nguyên dương thoả mãn.
Chọn đáp án A.
Cho hàm số y = f x có bảng biến thiên như hình vẽ bên
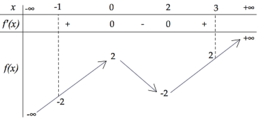
Có bao nhiêu số nguyên dương m để phương trình f 2 sin x + 1 = f ( m ) có nghiệm thực ?
A. 2.
B. 5.
C. 4.
D. 3.
Cho hàm số y = f(x) có đạo hàm f ' ( x ) = x - 1 2 x 2 - 2 x với ∀ x ∈ R . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số f ( x 2 - 8 x + m ) có 5 điểm cực trị?
A. 16
B. 18
C. 15
D. 17