Các câu hỏi tương tự
Cho hàm số
y
f
(
x
;
m
)
có đồ thị hàm số
y
f
(
x
;
m
)
như hình vẽ Biết
f
(
a
)
f
(
c
)
0
;
f
(
b
)
0
f
(
e
)
Hỏi hàm số...
Đọc tiếp
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
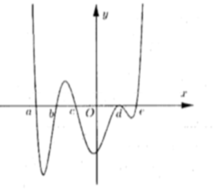
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số y = f(x). Hàm số y’ = f’(x) có bảng biến thiên như hình vẽ bên. Hàm số g(x) = f(x) – x có bao nhiêu điểm cực trị ?
![]()
A. 3
B. 2
C. 0
D. 1
Cho hàm số yf(x). Hàm số yf(x) có bảng biến thiên như hình vẽ dưới đâyHàm số g(x)f(x)-x có bao nhiêu điểm cực trị? A. 3 B. 2 C. 0 D. 1
Đọc tiếp
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như hình vẽ dưới đây
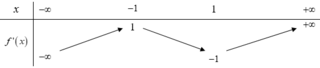
Hàm số g(x)=f(x)-x có bao nhiêu điểm cực trị?
A. 3
B. 2
C. 0
D. 1
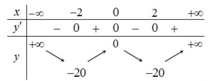
Cho hàm số f(x) có bảng biến thiên như hình vẽ dưới đây
Có bao nhiêu số nguyên m để hàm số y=f(x+m) nghịch biến trên khoảng (0;1).
A. 3.
B. 5.
C. 1.
D. 4.
Cho hàm số yf(x) có bảng biến thiên như hình vẽ bênCó bao nhiêu số nguyên dương m để phương trình f(2 sinx+1)f(m) có nghiệm thực ? A. 2. B. 5. C. 4. D. 3.
Đọc tiếp
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
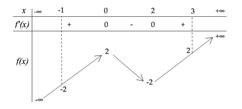
Có bao nhiêu số nguyên dương m để phương trình f(2 sinx+1)=f(m) có nghiệm thực ?
A. 2.
B. 5.
C. 4.
D. 3.
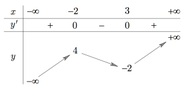
Cho hàm số f(x) có bảng biến thiên của hàm số yf(x) như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số
m
∈
-
10
;
10
để hàm số
y
f
3
x
-
1
+
x
3
-
3
m
x
đồng biến trên khoảng (-2;1)? A....
Đọc tiếp
Cho hàm số f(x) có bảng biến thiên của hàm số y=f'(x) như hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m ∈ - 10 ; 10 để hàm số y = f 3 x - 1 + x 3 - 3 m x đồng biến trên khoảng (-2;1)?
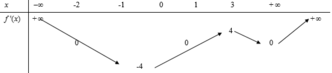
A. 8.
B. 6.
C. 7.
D. 5.
Hàm số f(x) có bảng biến thiên như hình vẽ sau
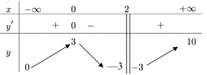
Hàm số f(x) có bao nhiêu điểm cực trị
A. 2.
B. 0.
C. 1.
D. 4.
Cho bảng biến thiên y = f ( x ) có bảng biến thiên như hình vẽ. Hàm số có bao nhiêu điểm cực trị?
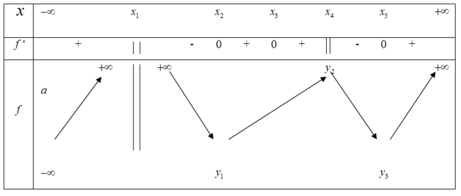
A. 4
B. 2
C. 3
D. 5
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(
a
,
b
,
c
,
d
∈
ℝ
)
có bảng biến thiên như hình sau:Tìm tất cả giá trị thực của tham số m để phương trình
m
f...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d ( a , b , c , d ∈ ℝ ) có bảng biến thiên như hình sau:
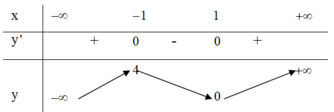
Tìm tất cả giá trị thực của tham số m để phương trình m = f ( x ) có 4 nghiệm phân biệt trong đó có đúng một nghiệm dương.
A.m > 2
B.0 < m < 4
C.m > 0
D.2 < m < 4