mấy bạn giúp mình nhanh nhanh với ạ

a: O nằm trên trung trực của AB,AC

=>OA=OB và OA=OC

=>OB=OC

mà AB=AC

nên AO là trung trực của BC

b: D nằm trên trung trực của AB

=>DA=DB

=>góc DAB=góc DBA

E nằm trên trung trực của AC

=>EA=EC

=>góc EAC=góc ECA=góc DBA=góc DAB

Xét ΔDAB và ΔEAC có

góc DAB=góc EAC

AB=AC

góc B=góc C

=>ΔDAB=ΔEAC

=>BD=CE

c: Xét ΔOBD và ΔOCE có

OB=OC

góc OBD=góc OCE

BD=CE

=>ΔOBD=ΔOCE

=>OD=OE

Giúp vs a

a: ΔABC cân tại A

mà AE là phân giác

nên AE là trung trực của BC

b: O nằm trên trung trực của AB

=>OA=OB

O nằm trên trung trực của BC

=>OB=OC

=>OA=OC

=>O nằm trên trung trực của AC

c: OA=OB=OC

=>O cách đều 3 đỉnh của ΔABC

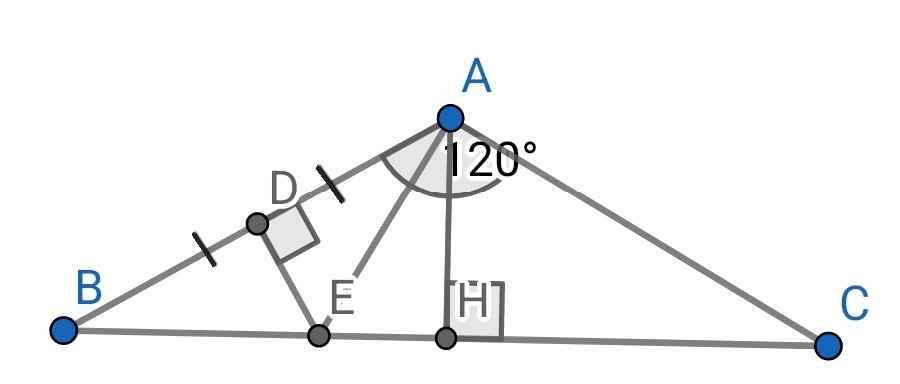 Do ∆ABC cân tại A (gt)

⇒ ∠B = ∠C = (180⁰ - ∠BAC) : 2

= (180⁰ - 120⁰) : 2

= 30⁰

∆AHB vuông tại H (do AH ⊥ BC)

⇒ ∠B + ∠BAH = 90⁰

⇒ ∠BAH = 90⁰ - ∠B

= 90⁰ - 30⁰

= 60⁰

Xét hai tam giác vuông: ∆AED và ∆BED có:

ED là cạnh chung

AD = BD (do D là trung điểm của AB)

⇒ ∆AED = ∆BED (hai cạnh góc vuông)

⇒ ∠EAD = ∠EBD = 30⁰ (hai góc tương ứng)

⇒ ∠EAH = ∠BAH - ∠EAD

= 60⁰ - 30⁰

= 30⁰

⇒ ∠EAH = ∠EAD

Xét hai tam giác vuông: ∆AEH và ∆AED có:

AE là cạnh chung

∠EAH = ∠EAD = 30⁰

⇒ ∆AEH = ∆AED (cạnh huyền - góc nhọn)

Mà ∆AED = ∆BED (cmt)

⇒ ∆BED = ∆AEH

a) \(\Delta ABC\)cân tại A có \(\widehat{BAC}=40^o\)nên \(\widehat{ABC}=\widehat{ACB}=70^o\)

gọi giao điểm của AB với đường trung trực của nó là O

CM : \(\Delta AOD=\Delta BOD\left(c.g.c\right)\)\(\Rightarrow\)\(\Delta ADB\)cân tại D

\(\Rightarrow\widehat{ABD}=\widehat{BAD}=70^o\); \(AD=BD\)( 1 )

\(\Rightarrow\widehat{A_1}=\widehat{C_1}=180^o-70^o=110^o\)

Xét  \(\Delta BEA\)và  \(\Delta CDA\)có :

AE = CD ( gt ) ; \(\widehat{A_1}=\widehat{C_1}\)( cmt ) ; AB = AC ( gt )

\(\Rightarrow\Delta BAE=\Delta ACD\left(c.g.c\right)\)\(\Rightarrow BE=AD\)( 2 )

b) Từ ( 1 ) và ( 2 ) suy ra BE = BD nên \(\Delta BED\)cân tại B

Mà \(\widehat{ADC}=180^o-2.70^o=40^o\)

\(\Rightarrow\widehat{BED}=\widehat{EDB}=40^o\)và \(\widehat{EBD}=100^o\)