Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: Phân giác BD
Những câu hỏi liên quan
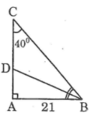
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 độ. Hãy tính các độ dài
a) AC
b) BC
c) Phân giác BD
Tam giác ABC vuông tại A có AB=21cm, góc \(C=40^0\). Hãy tính các độ dài
a) AC
b) BC
c) Phân giác BD
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: BC
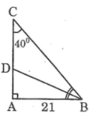
Tam giác ABC vuông tại A có AB = 21cm, góc C = 40 ° . Hãy tính các độ dài: AC
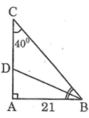
Tam giác ABC vuông tại A có \(AB=21cm,\widehat{C}=40^0\). Hãy tính các độ dài :
a) AC
b) BC
c) Phân giác BD
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,AB=21cm,góc C=40 độ .Tính
a,AC,BC b,Phân giác BD
a) Ta có:
\(sin40=\dfrac{AB}{BC}=\dfrac{21}{BC}\)\(\Rightarrow BC=\dfrac{21}{sin40}\simeq33cm\)
\(cos40=\dfrac{AC}{BC}\Rightarrow AC=cos40.33\simeq25cm\)
b) \(sinB=\dfrac{AC}{BC}=\dfrac{25}{33}\Rightarrow\widehat{B}\simeq49^o\)
\(BD=\dfrac{2.BC.AB.cos24,5}{BC+AB}\simeq12cm\)
Đúng 2
Bình luận (0)
\(Taco.\dfrac{BC}{sinA}=\dfrac{AB}{SinC}\Rightarrow BC=32,67cm=>AC=\sqrt{32,67^2-21^2}=25cm\)
Taco ^B=90-40=30 do
\(BD=\dfrac{2.21.32,67}{21+32,67}.CosB:2=24,69cm\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB=21cm,C=40 độ.Hãy tính độ dài :AC,BC,phân giác AD
Xét ΔABC vuông tại A có
tan C=AB/AC
=>21/AC=tan 40
=>\(AC\simeq25,03\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}\simeq32,67\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thắng qua D song song với AB cắt AC tại E. Tính độ dài các đoạn thẳng BD,DC và DE.
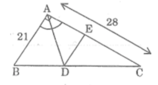
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 21 2 + 28 2 = 1225
Suy ra: BC = 35 (cm)
Vì AD là đường phân giác của ∠ (BAC) nên:
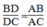(t/chất đường phân giác)
Suy ra: 
Hay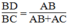 
Suy ra: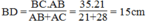 
Vậy DC = BC – BD = 35 – 15 = 20cm
Trong ΔABC ta có: DE // AB
Suy ra: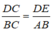 
(Hệ quả định lí Ta-lét)
Suy ra: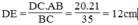 
Đúng 0
Bình luận (0)
Bài 1.Tam giác ABC vuông tại A, có AB 21cm, widehat{C} 40°, phân giác BD của góc ABC, D ∈ AC. Tínha) độ dài đoạn thẳng AC, BCb) độ dài đoạn thẳng BDBài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB 25cm, HC 64cm. Tính widehat{B}, widehat{C}Bài 3. Cho tam giác ABC vuông tại A có widehat{B} 30 °, AB 6cma) Giải tam giác vuông ABCb) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Đọc tiếp
Bài 1.Tam giác ABC vuông tại A, có AB = 21cm, \(\widehat{C}\) = 40°, phân giác BD của góc ABC, D ∈ AC. Tính
a) độ dài đoạn thẳng AC, BC
b) độ dài đoạn thẳng BD
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 25cm, HC = 64cm. Tính \(\widehat{B},\) \(\widehat{C}\)
Bài 3. Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30 °, AB = 6cm
a) Giải tam giác vuông ABC
b) Vẽ đường cao AH và trung tuyến Am của tam giác ABC. Tính diện tích tam giác AHM
Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)
Đúng 0
Bình luận (0)