Cho hình sau. So sánh các độ dài AB, AC, AD, AE.
Những câu hỏi liên quan
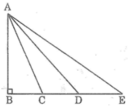
Bài 11 trang 38 sách bài tập Toán 7 Tập 2: Cho hình sau. So sánh các độ dài AB, AC, AD, AE.
Cho hình 1.
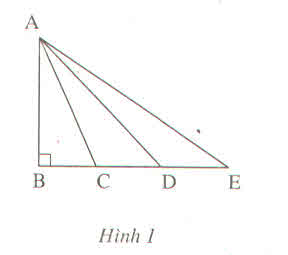
So sánh các độ dài AB, AC, AD, AE ?
Điểm C nằm giữa B và D nên BC < BD (1)
Điểm C nằm giữa B và E nên BD < BE (2)
Vì B, C, D, E thẳng hàng. Từ (1) và (2) suy ra
BC < BD < BE
AB⊥BE
Suy ra: AB < AC < AD < AE.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại B. Trên cạnh BC lấy các điểm D và E (D nằm giữa B và E).
a)So sánh độ dài các đoạn thẳng AB, AD, AE, AC.
b)Vẽ BI, BK, BH lần lượt vuông góc với AD, AE, AC. So sánh các góc ABH, ABK, ABI.
Cho tam giác ABC vuông tại B. Trên cạnh BC lấy các điểm D và E (D nằm giữa B và E).
a) So sánh độ dài các đoạn thẳng AB, AD, AE, AC
b) Vẽ BI, BK, BH lần lượt vuông góc với AD, AE, AC. So sánh các góc ABH, ABK, ABI.
Cho tam giác ABC vuông tại A. Các tia phân giác BM và CN cắt nhau tại I. Gọi D, E, F lần lượt là hình chiếu của điểm I xuống các cạnh AB, AC, BC.
a) So sánh AN và BN; AM và CN.
b) Chứng minh AD = AE.
c) Tính độ dài các đoạn thẳng AD, AE nếu AB = 8cm, AC = 15cm.
\
Cho tam giác ABC vuông tại B.Trên cạnh BC lấy các điểm D và E ( D nằm giữa B và E)
a) So sánh các độ dài các đoạn thẳng AB,AD,AE,AC
Vì ΔBAC vuông tại B
nên AB<AC
góc ACB<90 độ
=>góc ACD>90 độ
=>AC<AD
góc ACD>90 độ
=>góc CDA<90 độ
=>góc ADE>90 độ
=>AD<AE
=>AB<AC<AD<AE
Đúng 1
Bình luận (1)
cho tam giác ABC vuông ở A , các tia phân giác BM và CN cắt nhau tại I .gọi DEF là hình chiếu của đỉnh I xuống các cạnh AB, BC , AC.
a, so sánh AN và BN , AM và CM .
b, CMR AD = AE .
c , tính độ dài các đoạn AD và AE biết AB = 8 cm ,AC = 15 cm.
d, trong trường hợp tam giác ABC cân tại A , hãy chứng minh tam giác DEF cân
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đonạ thẳng AD, AE.
a) Hãy so sánh góc ADC và góc AEB.
b) Hãy so sánh các đoạn thẳng AD và AE.
ko cần vẽ hình đâu
xét tam giác ABC có : AC < AB
=> góc ABC < góc ACB (đl)
góc ABC + góc ABD = 180
góc ACB + góc ACE = 180
=> góc ACE < góc ABD
có tam giác ACE và tam giác ABD lần lượt cân tại C và B
=> góc E = (180 - góc ACE) : 2 và góc D = (180 - góc ABD) : 2 (đl)
=> góc E > góc D
Đúng 0
Bình luận (0)
a)
+ Trong ΔABC có: góc ABC đối diện cạnh AC, góc ACB đối diện cạnh AB.
b) ΔAED có:
⇒ AE < AD hay AD > AE
Đúng 0
Bình luận (0)
a, vì AC<AB nên suy ra \(\widehat{ADC}\)<\(\widehat{AEB}\)(góc đối diện với cạnh lớn hơn là góc lớn hơn)
b, vì AC<AB=> \(\widehat{ACB}\)>\(\widehat{ABC}\)(góc đối diện với cạnh lớn hơn là góc lớn hơn)
=> AD>AE
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
bài 10 Cho tam giác ABC cân tại A . Trên cạnh BC lấy các điểm BC lấy điểm D và E sao cho : BD=DE=EC. Gọi M là trung điểm của DE . 1) chứng minh AM vuông góc BC . 2) So sánh các độ dài AB,AD,AE,AC
a) Ta có: (hai góc kề bù)
(hai góc kề bù)
mà (hai góc ở đáy của ΔABC cân tại A)
nên
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Ta có: AD=AE(cmt)
nên A nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MD=ME(M là trung điểm của DE)
nên M nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của DE
hay (đpcm)
Đúng 0
Bình luận (0)