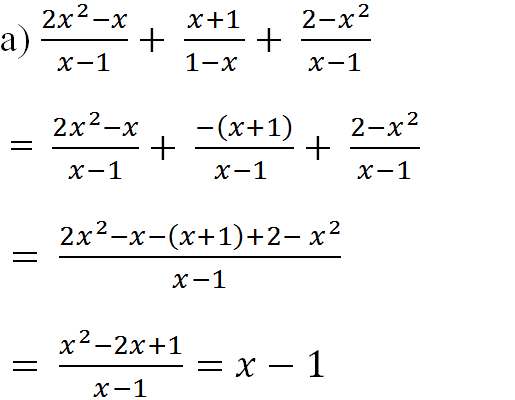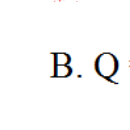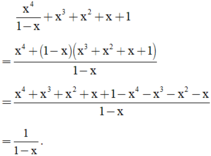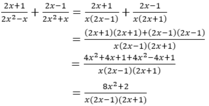Làm tính cộng các phân thức: 2 x + 1 2 x 2 - x + 32 x 2 1 - 4 x 2 + 1 - 2 x 2 x 2 + x

Những câu hỏi liên quan
áp dụng tính chất của phéo cộng các phân thức đại số đề làm phép tính sau:
\(\frac{2x}{x^2+4x+4}+\frac{x+1}{x+2}+\frac{2-x}{x^2+4x+4}\)
\(\frac{2x}{x^2+4x+4}+\frac{x+1}{x+2}+\frac{2-x}{x^2+4x+4}\)
\(=\frac{2x}{\left(x+2\right)^2}+\frac{\left(x+1\right)\left(x+2\right)}{\left(x+2\right)^2}+\frac{2-x}{\left(x+2\right)^2}\)
\(=\frac{2x+x^2+3x+2+2-x}{\left(x+2\right)^2}\)
\(=\frac{x^2+4x+4}{\left(x+2\right)^2}\)
\(=\frac{\left(x+2\right)^2}{\left(x+2\right)^2}\)
\(=1\)
Đúng 0
Bình luận (0)
Áp dụng quy tắc đổi dấu để các phân thức có cùng mẫu thức rồi làm tính cộng phân thức :
a) \(\dfrac{2x^2-x}{x-1}+\dfrac{x+1}{1-x}+\dfrac{2-x^2}{x-1}\)
b) \(\dfrac{4-x^2}{x-3}+\dfrac{2x-2x^2}{3-x}+\dfrac{5-4x}{x-3}\)
Phát biểu quy tắc : cộng hai phân thức cùng mẫu thức, cộng hai phân thức khác mẫu thức.
Làm tính cộng :
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
- Muốn cộng hai phân thức cùng mẫu, ta cộng các tử với nhau và giữ nguyên mẫu.
- Muốn cộng hai phân thức khác mẫu, ta quy đồng mẫu thức rồi cộng các phân thức cùng mẫu vừa tìm được.
\(\dfrac{3x}{x^3-1}+\dfrac{x-1}{x^2+x+1}\)
\(=\dfrac{3x}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x+x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{1}{x-1}\)
Đúng 0
Bình luận (0)
Làm tính cộng các phân thức
a) 11x+13/3x-3 + -15x-17/4x-4
b) 2x+1/2x2-x + -32x2/4x2-1 + 1-2/2x2+x
Làm tính cộng phân thức :
\(\frac{x^4}{1-x}+x^3+x^2+1\)
ĐK: x#0; x#-1
\(\frac{x^4}{1-x}\)+ x3 + x2 + 1
= \(\frac{x^4}{1-x}\)+ \(\frac{x^3\left(1-x\right)}{1-x}\)+ \(\frac{x^2\left(1-x\right)}{1-x}\)+ \(\frac{1-x}{1-x}\)
= \(\frac{x^4+x^3-x^4+x^2-x^3+1-x}{1-x}\)
= \(\frac{x+1}{1-x}\)
Đúng 0
Bình luận (0)
Làm tính cộng các phân thức: x 4 1 - x + x 3 + x 2 + x + 1
Làm tính cộng các phân thức:
1
x
2
+
x
+
1
+
1
x
2
-
x
+
2
x
1
-
x
3
Đọc tiếp
Làm tính cộng các phân thức: 1 x 2 + x + 1 + 1 x 2 - x + 2 x 1 - x 3
Làm phếp tính cộng các phân thức sau 2x-3y/xy-y²+1/x-y
\(=\dfrac{2x-3y}{y\left(x-y\right)}+\dfrac{1}{x-y}=\dfrac{2x-3y+y}{y\left(x-y\right)}=\dfrac{2x-2y}{y\left(x-y\right)}=\dfrac{2}{y}\)
Đúng 0
Bình luận (0)
\(\dfrac{2x-3y}{xy-y^2}+\dfrac{1}{x-y}=\dfrac{2x-3y}{y\left(x-y\right)}+\dfrac{1}{x-y}=\dfrac{2x-3y+y}{y\left(x-y\right)}=\dfrac{2x-2y}{y\left(x-y\right)}=\dfrac{2}{y}.\)
Đúng 0
Bình luận (0)
Làm tính cộng các phân thức 2 x + 1 2 x 2 - x + 2 x - 1 2 x 2 + x