Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Những câu hỏi liên quan
26 tháng 2 2017 lúc 19:38
tính cảm ứng từ tại tâm của 2 vòng tròn dây dẫn đồng tâm , bán kính mỗi vòng là R=8cm , vòng kia là 2R , trong mỗi vòng có dòng điện cường độ I=10A chạy qua . xét các trường hợp sau :
a) 2 vòng nằm trong cùng 1 mặt phẳng , 2 dòng điện cùng chiều .
b) 2 vòng nằm trong cùng 1 mặt phẳng , 2 dòng điện ngược chiều .
c) 2 vòng nằm trong 2 mặt phẳng vuông góc với nhau
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
+
6
y
-
4
z
-
2
0
mặt phẳng
α
:
x
+
4
y
+
z
-
11
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 mặt phẳng α : x + 4 y + z - 11 = 0 . Gọi (P) là mặt phẳng vuông góc với (a), (P) song song với giá của véctơ v → = 1 ; 6 ; 2 và (P) tiếp xúc với (S). Lập phương trình mặt phẳng (P).
A. 2x - y + 2z - 2 = 0 và x - 2y + z - 21 = 0
B. x - 2y + 2z + 3 = 0 và x - 2y + z - 21 = 0
C. 2x - y + 2z + 3 = 0 và 2x - y + 2z - 21 = 0
D. 2x - y + 2z + 5 = 0 và 2x - y + 2z - 2 = 0
Đáp án C
Ta có: n P → = n α → ; n P → = 2 ; - 1 ; 2 ⇒ P : 2 x - y + 2 z + D = 0
Mặt cầu (S) có tâm I 1 ; - 3 ; 2 ; R = 4 ⇒ d I ; P = 4 ⇔ 9 + D 4 + 1 + 4 = 4 ⇔ [ D = 3 D = - 21
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu
S
:
x
2
+
y
2
+
z
2
-
2
x
+
6
y
-
4
z
-
2
0
,mặt phẳng
(
α
)
:
x
+
4
y
+
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 ,mặt phẳng ( α ) : x + 4 y + z - 11 = 0 .Gọi (P) là mặt phẳng vuông góc với α , (P) song song với giá của véctơ v → = 1 ; 6 ; 2 và (P) tiếp xúc với (S). Lập phương trình mặt phẳng (P)
A. 2x - y + 2z - 2 = 0 và x - 2y + z - 21 = 0.
B. x - 2y + 2z + 3 = 0 và x - 2y + z - 21 = 0.
C. 2x - y + 2z + 3 = 0 và 2x - y + 2z - 21 = 0.
D. 2x - y + 2z + 5 = 0 và 2x - y + 2z - 2 = 0.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
−
2
x
+
6
y
−
4
z
−
2
0
,
mặt phẳng
α
:
x
+
4
y
+
z
−
11...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x + 6 y − 4 z − 2 = 0 , mặt phẳng α : x + 4 y + z − 11 = 0. Gọi (P) là mặt phẳng vuông góc với α , P song song với giá của vecto v → 1 ; 6 ; 2 v à P tiếp xúc với (S). Lập phương trình mặt phẳng ( P ).
A. 2 x − y + 2 z − 2 = 0 và x − 2 y + z − 21 = 0
B. x − 2 y + 2 z + 3 = 0 và x − 2 y + z − 21 = 0
C. 2 x − y + 2 z + 3 = 0 và 2 x − y + 2 z − 21 = 0
D. 2 x − y + 2 z + 5 = 0 và x − 2 y + 2 z − 2 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
(
S
)
:
x
2
+
y
2
+
z
2
-
2
x
+
6
y...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 2 x + 6 y - 4 z - 2 = 0 mặt phẳng ( α ) : x + 4 y + z - 11 = 0 . Gọi (P) là mặt phẳng vuông góc với ( α ) , (P) song song với giá của vecto v → = ( 1 ; 6 ; 2 ) và (P) tiếp xúc với (S). Lập phương trình mặt phẳng ( P ).
A. 2x -y +2z -2 = 0 và x - 2y + z -21 = 0
B. x- 2y+ 2z + 3 = 0 và x - 2y + z -21 = 0
C. 2x -y +2z + 3 = 0 và 2x - y + 2z -21 = 0
D. 2x -y +2z + 5 = 0 và x - 2y + 2z -2 = 0
Đáp án C
Ta có:
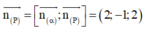
Mặt cầu (S) có tâm I(1;-3;2); R =4
Đúng 0
Bình luận (0)
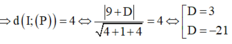
Trong 4 cách sau :
1. Giảm chiều cao kê mặt phẳng nghiêng
2. Tăng chiều cao kê mặt phẳng nghiêng
3. Giảm độ dài của mặt phẳng nghiêng
4. Tăng độ dài của mặt phẳng nghiêng
Các cách nào làm giảm độ nghiêng của mặt phẳng nghiêng ?
A. Các cách 1 và 3
B. Các cách 1 và 4
C. Các cách 2 và 3
D. Các cách 2 và 4
Trong 4 cách sau :
1. Giảm chiều cao kê mặt phẳng nghiêng
2. Tăng chiều cao kê mặt phẳng nghiêng
3. Giảm độ dài của mặt phẳng nghiêng
4. Tăng độ dài của mặt phẳng nghiêng
Các cách nào làm giảm độ nghiêng của mặt phẳng nghiêng ?
A. Các cách 1 và 3
B. Các cách 1 và 4
C. Các cách 2 và 3
D. Các cách 2 và 4
cho hình bình hành abcd và tam giác scd nằm trong 2 mặt phẳng khác nhau gọi i là trung điểmcủa sd và k thuộc sc sao cho sk/sc = 1/3 mặt phẳng p đi qua ik và song song vs ac cắt mặt abcd theo 1 giao tuyến
27 tháng 4 2017 lúc 20:16
tính cảm ứng từ tại tâm của 2 vòng dây dẫn đồng tâm , có bán kính là R và 2R . trong mỗi vòng tròn có dòng điện I=10A chạy qua . biết R=8cm . xét các trường hợp :
a) hai vòng tròn nằm trong cùng 1 mặt phẳng , 2 dòng điện chạy cùng chiều .
b) hai vòng tròn nằm trong cùng 1 mặt phẳng , 2 dòng điện chạy ngược chiều .
c) hai vòng tròn nằm trong 2 mặt phẳng vuông góc nhau .
25 tháng 2 2017 lúc 16:37
2 vòng dây dẫn bán kính như nhau và bằng 5cm , các vòng dây có dòng điện I1=2A , I2=1A . vòng dây 1 đặt trong mặt phẳng ngang , vòng dây 2 đặt trong mặt phẳng thẳng đứng , tâm 2 vòng dây trùng nhau . tìm B tại tâm 2 vòng
chứng minh bằng pp quy nạp
trong một mặt phẳng, n đường thẳng đôi một cắt nhau và không có đường thẳng nào đồng quy thì chúng chia mặt phẳng thành \(\frac{n^2+n+2}{2}\) miền phẳng