Các câu sau đúng hay sai?
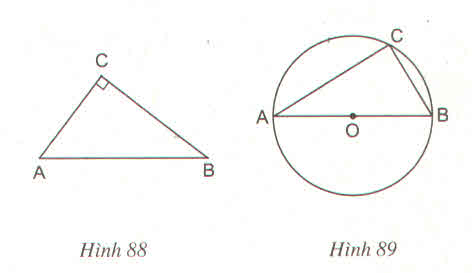
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)
b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).
Những câu hỏi liên quan
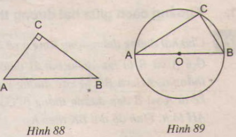
Các câu sau đúng hay sai :
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)
b) Nếu điểm C thuộc đường tròn có đường kính AB (C khác A và B) thì tam giác ABC vuông tại C (h.89)
Bài giải:
a) Đúng.
Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền nên
OC = 1212AB hay OC = OA = OB. Nên A, B, C cùng thuộc đường tròn bán kình OA. Vậy C thuộc đường tròn đường kính AB.
b) Đúng.
Gọi O là tâm đường tròn. Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do CO = AO = OB) nên tam giác ABC vuông tại C.
Đúng 1
Bình luận (0)
a) Đúng.
Gọi O là trung điểm của AB. Ta có CO là trung tuyến ứng với cạnh huyền nên
OC = \(\dfrac{1}{2}\)AB hay OC = OA = OB. Nên A, B, C cùng thuộc đường tròn bán kình OA. Vậy C thuộc đường tròn đường kính AB.
b) Đúng.
Gọi O là tâm đường tròn. Tam giác ABC có trung tuyến CO bằng nửa cạnh AB (do CO = AO = OB) nên tam giác ABC vuông tại C.
Đúng 0
Bình luận (0)
Xét tính đúng – sai của mỗi khẳng định sau:
Cho tam giác ABC nội tiếp đường tròn (O).
a) Nếu BC là đường kính của đường tròn thì ∠ (BAC) = 90 °
b) Nếu AB = AC thì AO vuông góc với BC.
c) Nếu tam giác ABC không vuông thì điểm O nằm bên trong tam giác đó.
Chứng minh rằng: nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có bán bán kính là AB.
Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng
∠
ACB 90
°
Khẳng định nào sau đây là đúng?A. AB luôn là đường kính của mặt cầu đã cho.B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC.C. Tam giác ABC vuông cân tại C.D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.
Đọc tiếp
Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng ∠ ACB = 90 °
Khẳng định nào sau đây là đúng?
A. AB luôn là đường kính của mặt cầu đã cho.
B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC.
C. Tam giác ABC vuông cân tại C.
D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.
Chọn B.
Mặt phẳng (ABC) cắt mặt cầu theo đường tròn ngoại tiếp tam giác ABC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A(AB>AC) có đường cao AH (H thuộc BC).Trên nửa mp bờ BC chứa điểm A,vẽ nửa đường tròn(O1) đường kính BH cắt AB tại I (I khác B) và nửa đường tròn (O2) đường kính HC cắt AC tại K (K khác C).CM
a) Tứ giác BIKC là tứ giác nội tiếp
b) IK là tiếp tuyến chung của 2 nửa đtron (O1) và (O2)
Giúp mình với ạ,mình cảm ơn rất nhiềuuuuuu
a: góc HIB=1/2*sđ cung HB=90 độ
=>HI vuông góc AB
góc CKH=1/2*sđ cung CH=90 độ
=>HK vuông góc AC
góc AIH=góc AKH=góc KAI=90 độ
=>AIHK là hình chữ nhật
=>góc AIK=góc AHK=góc C
=>góc KIB+góc KCB=180 độ
=>KIBC nội tiếp
b: góc O1IK=góc O1IH+góc KIH
=góc O1HI+góc KAH
=góc HAC+góc HCA=90 độ
=>IK làtiếp tuyến của (O1)
góc O2KI=góc O2KH+góc IKH
=góc O2HK+góc IAH
=góc HAB+góc HBA=90 độ
=>IK là tiếp tuyến của (O2)
Đúng 0
Bình luận (0)
Xét tính đúng - sai của mỗi khẳng định sau :
Cho tam giác ABC nội tiếp đường tròn (O)
a) Nếu BC là đường kính của đường tròn thì \(\widehat{BAC}=90^0\)
b) Nếu AB = AC thì AO vuông góc với BC
c) Nếu tam giác ABC không vuông thì điểm O nằm bên trong tam giác đó
Cho tam giác ABC có hai đường cao BE, CF cắt nhau tại H. Gọi E là điểm đối xứng H qua AC, F là điểm đối xứng H qua AB. Chứng minh:a, Tứ giác BCEF nội tiếp đường tròn (O)b, Năm điểm A, F, B, C, E cùng thuộc một đường trònc, AO và EF vuông góc nhaud, Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi
Đọc tiếp
Cho tam giác ABC có hai đường cao BE, CF cắt nhau tại H. Gọi E' là điểm đối xứng H qua AC, F' là điểm đối xứng H qua AB. Chứng minh:
a, Tứ giác BCE'F' nội tiếp đường tròn (O)
b, Năm điểm A, F', B, C, E' cùng thuộc một đường tròn
c, AO và EF vuông góc nhau
d, Khi A chạy trên (O) thì bán kính đường tròn ngoại tiếp tam giác AEF không đổi
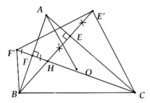
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi
Đúng 1
Bình luận (1)
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
c) Tính độ dài cạnh BC và bán kính đường tròn ngoại tiếp tam giác ABC theo b, c.
c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c
Đúng 0
Bình luận (0)
Bài 1. Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB. Tính số đo các góc cònlại của tam giác ABC nếu biết Ab 40◦Bài 3. Cho đường tròn (O;R), các điểm A,B thuộc (O) sao choAOB 90◦.(a) Tính độ dài AB theo R.(b) Gọi H là trung điểm AB. Chứng minh OH ⊥ AB.Bài 4. Cho hình vuông ABCD có AB asqrt{2}(a) Chứng minh bốn điểm A,B,C,D cùng thuộc một đường tròn.(b) Tính bán kính của đường tròn đi qua A,B,C,D theo a.
Đọc tiếp
Bài 1. Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB. Tính số đo các góc còn
lại của tam giác ABC nếu biết Ab = 40◦
Bài 3. Cho đường tròn (O;R), các điểm A,B thuộc (O) sao choAOB = 90◦
.
(a) Tính độ dài AB theo R.
(b) Gọi H là trung điểm AB. Chứng minh OH ⊥ AB.
Bài 4. Cho hình vuông ABCD có AB = a\(\sqrt{2}\)
(a) Chứng minh bốn điểm A,B,C,D cùng thuộc một đường tròn.
(b) Tính bán kính của đường tròn đi qua A,B,C,D theo a.