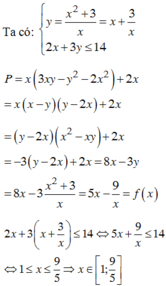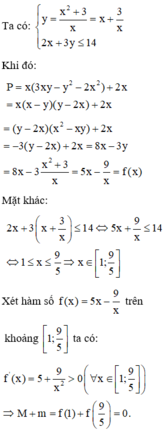Gía trị nhỏ nhất của x2-4x căn 2x +14=0

Những câu hỏi liên quan
Gía trị nguyên nhỏ nhất của m để pt mx2-4x+4=0 có duy nhất 1 nghiệm là ?
Là 0 đó bạn , câu này lừa tình ở chỗ nếu m=0 thì ko xét được delta! thằng nào ngu m=1 là sai!=))
Đúng 0
Bình luận (0)
Bạn Trần Xuân Bão Cảm Xúc ơi dó là pt bậc hai nên điều kiện là m khác 0 dó bạn ạ. Nên suy nghĩ kĩ trước khi phán xét người khác nhé
Đúng 0
Bình luận (0)
Cho x,y0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3
y
-...
Đọc tiếp
Cho x,y>0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Ta có:
x 2 - x y + 3 = 0 1 2 x + 3 y - 14 ≤ 0 2
Do x,y>0 nên ⇔ x 2 + 3 x thay vào (2) ta được:
2 x + 3 . x 2 + 3 x - 14 ≤ 0
⇔ 2 x 2 + 3 x 2 + 9 - 14 x x ≤ 0
⇔ 5 x 2 - 14 x + 9 ≤ 0 ⇔ 1 ≤ x ≤ 9 5
Thay y = x 2 + 3 x vào P ta được:
P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
= 3 x 2 . x 2 + 3 x - x . x 2 + 3 x 2 - 2 x 3 + 2 x
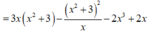
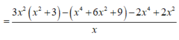
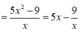
P ' = 5 + 9 x 2 > 0 với mọi x nên hàm số P=P(x) đồng biến trên 1 ; 9 5
Vậy 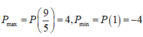
Tổng ![]() .
.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho x,y 0 và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
2
y
-...
Đọc tiếp
Cho x,y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 2 y - 14 ≤ 0 .Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x
A. 4.
B. 8.
C. 12.
D. 0.
Cho
x
,
y
0
và thỏa mãn
x
2
−
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 − x y + 3 = 0 2 x + 3 y − 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y − x y 2 − 2 x 3 + 2 x ?
A. 4
B. 8
C. 12
D. 0
Cho
x
,
y
0
và thỏa mãn
x
2
-
x
y
+
3
0
2
x
+
3...
Đọc tiếp
Cho x , y > 0 và thỏa mãn x 2 - x y + 3 = 0 2 x + 3 y - 14 ≤ 0 . Tính tổng giá trị lớn nhất và nhỏ nhất của biểu thức P = 3 x 2 y - x y 2 - 2 x 3 + 2 x ?
A. 8
B. 0
C. 4
D. 12
Đáp án B
Phương pháp:
- Rút y từ phương trình đầu, thay vào bất phương trình sau tìm điều kiện của x .
- Thay y ở trên vào biểu thức P đưa về biến x .
- Sử dụng phương pháp hàm số đánh giá P tìm GTLN, GTNN.
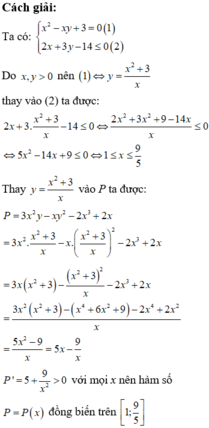
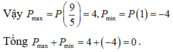
Đúng 0
Bình luận (0)
chỉ mình câu này với
rút gon biểu thức A= x^2+2x/ x^2-4x+4 : ( x+2/x-1/2-x+6-x^2/x^2-2x) với x khác 0,2,-2
rút gọn A
tính giá trị của A biết I 2x +1 I =3
tìm x để A<0 , tìm giá trị x nguyên để A nhận giá trị nguyên , tìm gía trị nhỏ nhất của với x>2
Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức:
a) A= căn 4x2-16x+20
b) B= căn x2+2x+10 cộng căn 2x2+4x+3
\(A=\sqrt{4x^2-16x+20}=2\sqrt{x^2-4x+5}=2\sqrt{\left(x-2\right)^2+1}\ge2\)
Dấu "=" xảy ra khi x = 2
Min A = 2 <=> x = 2
Câu b) bạn ghi rõ đề hơn nhé.
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất P = căn(2x^2 + 2x + 1) + căn(2x^2 - 4x + 4)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bạc hai y = -2x2 + 4x + 3
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = -3x2 + 2x + 1 trên (1;3)
tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bậc hai y = x2 - 4x - 5 trên (-1;4)
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Đúng 0
Bình luận (0)
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
Đúng 0
Bình luận (0)
Câu 3:
$y=x^2-4x-5$ có $a=1>0, b=-4; c=-5$ có trục đối xứng $x=\frac{-b}{2a}=2$
Do $a>0$ nên hàm nghịch biến trên $(-\infty;2)$ và đồng biến trên $(2;+\infty)$
Với $x\in (-1;4)$ vẽ BTT ta thu được $y_{\min}=f(2)=-9$
Đúng 0
Bình luận (0)