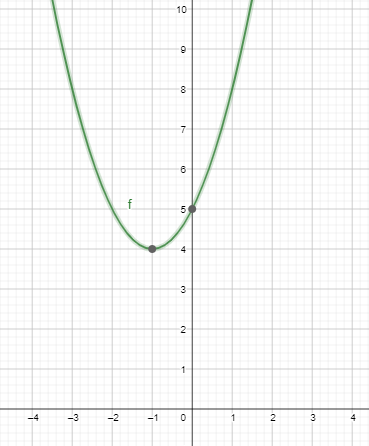
1/Xét sự biến thiên và vẽ đồ thị hàm số 𝑦=𝑥2−2𝑥−3 .
Những câu hỏi liên quan
Cho hai hàm số: 𝑦 = 𝑥 + 1 (𝐷1) và 𝑦 = 3 − 2𝑥 (𝐷2) :
a) Vẽ (D1) và (D2) trên cùng một hệ trục tọa độ.
b) Xác định giao điểm của hai đồ thị bằng phép tính.
\(b,\text{PT hoành độ giao điểm: }x+1=3-2x\Leftrightarrow x=\dfrac{2}{3}\Leftrightarrow y=\dfrac{5}{3}\Leftrightarrow A\left(\dfrac{2}{3};\dfrac{5}{3}\right)\\ \text{Vậy }A\left(\dfrac{2}{3};\dfrac{5}{3}\right)\text{ là giao 2 đths}\)
Đúng 3
Bình luận (0)
Vẽ đồ thị hàm số sau :
𝑦 = 𝑥\(^2\) + 2𝑥 + 5
Cho hàm số bậc nhất 𝑦(𝑚−2)𝑥+𝑚+3(𝑑)a. Tìm m để hàm số đồng biến, nghịch biến.b. Tìm m để(d) đi qua điểm A (1; 2)c. Tìm m để đồ thị hàm số song song với đường thẳng 𝑦3𝑥−3+𝑚(𝑑1)d. Tìm m để đồ thị hàm số đã cho vuông góc với đường thẳng 𝑦2𝑥+1(𝑑2)e. Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3.f. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3.g. Tìm m biết (d) tạo với trục hoành một góc 45𝑜.
Đọc tiếp
Cho hàm số bậc nhất 𝑦=(𝑚−2)𝑥+𝑚+3(𝑑)
a. Tìm m để hàm số đồng biến, nghịch biến.
b. Tìm m để(d) đi qua điểm A (1; 2)
c. Tìm m để đồ thị hàm số song song với đường thẳng 𝑦=3𝑥−3+𝑚(𝑑1)
d. Tìm m để đồ thị hàm số đã cho vuông góc với đường thẳng 𝑦=2𝑥+1(𝑑2)
e. Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 3.
f. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3.
g. Tìm m biết (d) tạo với trục hoành một góc 45𝑜.
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Xét sự biến thiên và vẽ đồ thị của hàm số y=|-3x+3|
(giúp em với mọi người ,gấp lắm ạ)
hàm số tăng trên khoảng [1;+\(\infty\))
Hàm số giảm trên khoảng(-\(\infty\);-1)
Đúng 0
Bình luận (0)
Câu 3: Xác định hàm số 𝑦=𝑎𝑥2+2𝑥+𝑐 biết đồ thị có tung độ đỉnh là 6 và đi qua điểm A(1;-4)
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+c+2=-4\\-\dfrac{4-4ac}{4a}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-6-c\\4ac-4=24a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-6-c\\4c\left(-6-c\right)-4-24\left(-6-c\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-c-6\\-24c+4c^2-4+144+24c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-c-6\\4c^2+140=0\end{matrix}\right.\)(vô lý)
Đúng 0
Bình luận (0)
xét sự biến thiên và vẽ đồ thị hàm số: y = \(\sqrt[3]{x}\)
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
c) Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.
a) y = 4 x 3 + x, y′ = 12 x 2 + 1 > 0, ∀ x ∈ R
Bảng biến thiên:
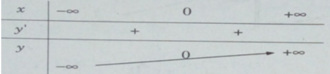
Đồ thị:
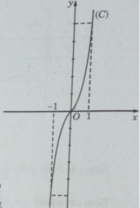
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì f′(x0) = 12 x 0 2 + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x0 = 1 hoặc x0 = -1
Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8
c) Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔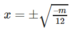 
Từ đó suy ra:
y’ > 0 với
y’ < 0 với
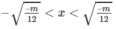
Vậy hàm số (1) đồng biến trên các khoảng
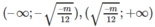
và nghịch biến trên khoảng
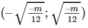
Đúng 0
Bình luận (0)
Xét chiều biến thiên và vẽ đồ thị của các hàm số: y = 1 2 x - 1
Hàm s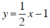ố 
có:
+ Tập xác định D = R.
+ Có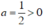 
nên hàm số đồng biến trên R.
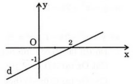
+ Tại x = 0 thì y = 1/2 . 0 – 1 = –1 . Vậy A (0; –1) thuộc đồ thị hàm số.
Tại x = 2 thì y = 1/2 . 2 – 1 = 0. Vậy B (2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A (0; –1) và B (2; 0).
Đúng 0
Bình luận (0)
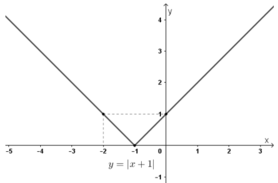
Xét chiều biến thiên và vẽ đồ thị của các hàm số: y = |x + 1|
Hàm số y = |x + 1|
Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.
Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1.
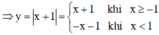
+ Tập xác định: R
+ Trên (–∞; –1), y = x + 1 đồng biến.
Trên (–1 ; +∞), y = –x – 1 nghịch biến.
Ta có bảng biến thiên :
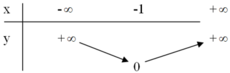
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.
Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.
Đúng 0
Bình luận (0)