Cho hình bình hành ABCD. Tổng các vectơ A B → + A C → + A D → là
![]()
![]()
![]()
![]()
Cho hình bình hành ABCD có tâm là O . Tìm các vectơ từ 5 điểm A B C D O a). Bằng vectơ AB ; OB. b). Có độ dài bằng OB .
Bằng \(\overrightarrow{AB}\) là \(\overrightarrow{DC}\)
Bằng \(\overrightarrow{OB}\) là \(\overrightarrow{DO}\)
Có độ dài bằng OB là \(\overrightarrow{OB};\overrightarrow{BO};\overrightarrow{OD};\overrightarrow{DO}\)
a) Bằng vectơ AB :
\(\overrightarrow{DC}\)
Bằng vectơ OB :
\(\overrightarrow{DO}\)
b)Có độ dài bằng OB :
\(\overrightarrow{OD},
\overrightarrow{DO},
\overrightarrow{BO}\)
Cho hình bình hành ABCD. A B → + A C → + A D → Tổng các vectơ là
A. A C →
B. 2
C . 3
D. 5
Cho hình bình hành ABCD có O = AC n BD a,Tìm các vectơ khác vectơ O + Cùng phương với vectơ OA + Cùng chiều với vectơ BD b, Tìm các vectơ + bằng với AB + bằng với CO
Câu 8: Cho hình bình hành ABCD tâm O. Các vectơ khác 0 ngược hướng với OB là
A. BD OD , . B. BD OD BO , , . C. DB DO , . D. BD BO , .
Câu 9: Cho ba điểm A, B, C thẳng hàng, trong đó điểm B nằm giữa hai điểm A và C. Khi đó các cặp vectơ nào sau đây cùng hướng?
A. CB và AB. B. AB và AC. C. AB và CB . D. BA và BC.
Câu 10: Cho một đa giác 1 2 2019 A A A ... có 2019 cạnh. Số vectơ khác 0 có điểm đầu và điểm cuối được tạo thành từ các đỉnh của đa giác
A. 4074342. B. 8148684. C. 4076361. D. 8152722
Cho hình bình hành ABCD hai điểm M và N lần lượt là trung điểm của BC và AD. Vẽ điểm E sao cho \(\overrightarrow {CE} = \overrightarrow {AN} \) (hình 1)
a) Tìm tổng của các vectơ:
\(\overrightarrow {NC} \) và \(\overrightarrow {MC} \); \(\overrightarrow {AM} \) và \(\overrightarrow {CD} \); \(\overrightarrow {AD} \) và \(\overrightarrow {NC} \)
b) Tìm các vectơ hiệu:
\(\)\(\overrightarrow {NC} - \overrightarrow {MC} \); \(\overrightarrow {AC} - \overrightarrow {BC} \); \(\overrightarrow {AB} - \overrightarrow {ME} \).
c) Chứng minh \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \)
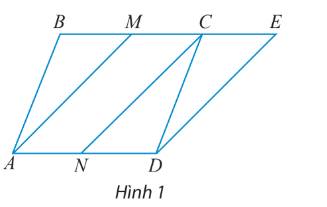
a) Ta có: \(\overrightarrow {CE} = \overrightarrow {AN} \Rightarrow CE//AN\) và \(CE = AN = ND = BM = MC\)
Suy ra \(\overrightarrow {MC} = \overrightarrow {CE} \)
+) \(\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CE} = \overrightarrow {NE} \)
+) ABCD là hình bình hành nên \(\overrightarrow {CD} = \overrightarrow {BA} \)
\(\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BM} \)
+) Ta có \(\overrightarrow {MC} = \overrightarrow {AN} \Rightarrow AMCN\) là hình bình hành nên \(\overrightarrow {NC} = \overrightarrow {AM} \)
\(\overrightarrow {AD} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {AM} = \overrightarrow {AE} \) (vì AMED là hình bình hành)
b) Ta có:
+) \(\overrightarrow {NC} - \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {CM} = \overrightarrow {NM} \)
+) \(\overrightarrow {AC} - \overrightarrow {BC} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
+) \(\overrightarrow {AB} - \overrightarrow {ME} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DB} \)
c) Ta có:
\(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AM} + \overrightarrow {MC} = \overrightarrow {AC} \)
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Từ đó suy ra \(\overrightarrow {AM} + \overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {AD} \) (đpcm)
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
1: ABCD là hình bình hành
=>\(\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}\)
\(\overrightarrow{AB}+\overrightarrow{DA}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}\)
2: \(\overrightarrow{AC}-\overrightarrow{ED}+\overrightarrow{CD}+\overrightarrow{EC}-\overrightarrow{BC}\)
\(=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CB}\)
\(=\overrightarrow{AD}+\overrightarrow{DE}+\overrightarrow{EC}+\overrightarrow{CB}\)
\(=\overrightarrow{AE}+\overrightarrow{EC}+\overrightarrow{CB}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}\)
3:
a: \(\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}\)
\(=-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{0}\)
\(\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}\)
\(=\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}\)
\(=\overrightarrow{CB}+\overrightarrow{BC}=\overrightarrow{0}\)
Gọi H là trung điểm của BC
Xét ΔABC có AH là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AH}\)
b: ABCD là hình vuông
=>\(DB^2=DA^2+AB^2\)
=>\(DB^2=a^2+a^2=2a^2\)
=>\(DB=a\sqrt2\)
ABCD là hình vuông
=>\(\overrightarrow{DA}+\overrightarrow{DC}=\overrightarrow{DB}\)
=>\(\left|\overrightarrow{DA}+\overrightarrow{DC}\right|=DB=a\sqrt2\)
\(\overrightarrow{AB}-\overrightarrow{CB}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
=>\(\left|\overrightarrow{AB}-\overrightarrow{CB}\right|=CA=a\sqrt2\)
Cho hình thang ABCD ( AB // CD ) và điểm M nằm trong hình thang ABCD. Kẻ các hình bình hành MAED, MBFC. Chứng minh hai vectơ EF và vectơ AB cùng phương.
Cho hai hình bình hành ABCD và EBEF với A, D, F không thẳng hàng. Dựng các vectơ \(\overrightarrow{EH}\) và \(\overrightarrow{FG}\) bằng vectơ \(\overrightarrow{AD}\). Chứng minh tứ giác CDGH là hình bình hành ?

\(\overrightarrow{EH}=\overrightarrow{AD},\overrightarrow{FG}=\overrightarrow{AD}\Rightarrow\overrightarrow{EH}=\overrightarrow{FG}\)
=> Tứ giác FEHG là hình bình hành
=> \(\overrightarrow{GH}=\overrightarrow{FE}\) (1)
Ta có \(\overrightarrow{DC}=\overrightarrow{AB},\overrightarrow{AB}=\overrightarrow{FE}\)
=> \(\overrightarrow{DC}=\overrightarrow{FE}\) (2)
Từ (1) và (2) ta có \(\overrightarrow{GH}=\overrightarrow{DC}\)
Vậy tứ giác GHCD là hình bình hành.
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ B B ' → , C C ' → , D D ' → đồng phẳng.
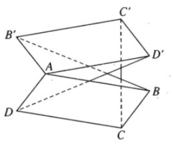
Ta có: 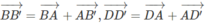
Do đó: 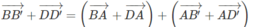
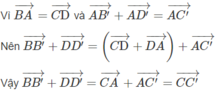
Hệ thức 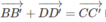
biểu thị sự đồng phẳng của ba vectơ B B ' → , C C ' → , D D ' →