Cho hàm số xác định bởi y = f ( x ) = 40 x + 20 , Với giá tri nào của x thì f ( x ) = 300 ?
A. x = 7
B. x = 70
C. x = 17
D. x = 140
Cho hàm số xác định bởi y = f ( x ) = − 4 x − 2020 . Với giá tri nào của x thì f ( x ) = − 2040 ?
A. x = 5
B. x = 50
C. x = 1015
D. x = 80
Cho hàm số y = f(x) xác định bởi công thức : y = f(x) =\(\dfrac{2}{3}\)x+6
Tính các giá trị của x tương ứng với giá trị của y = 5, y = –4
y=5
=>2/3x=-1
hay x=-3/2
y=-4
=>2/3x=-10
hay x=-15
Câu 34: Số 36 có căn bậc hai là:
A. 6 B. -6
C. 6 và -6 D. 62
Câu 35: Cho hàm số xác định bởi y = f(x) = 40x + 20, Với giá tri nào của x thì f(x) = 300?
A. x = 7 B. x = 70
C. x = 17 D. x = 140
Câu 36: R ∩ Q =
A. R B. Q
C. ∅ D. I
Câu 36: Đồ thị hàm số y = ax (a ≠ 0) là:
A. Một đường thẳng C. Một đoạn thẳng đi qua gốc tọa độ
B. Đi qua gốc tọa độ D. Một đường thẳng đi qua gốc tọa độ
Câu 37: Điểm thuộc đồ thị hàm số y = -2x là:
A. M (-2;-2) B. N (1;4)
C. P (-1;-2) D. Q (-1;2)
Câu 38: Điểm B(-2;6) không thuộc đồ thị hàm số:
A. y = -3x B. y = x+8
C. y = 4-x D. y = x
Câu 39: Đồ thị hàm số y = -2,5x là đường thẳng OB với O(0;0) và:
A. B (-2;-5) B. B (5;-2)
C. B (2;-5) D. B (4;10)
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
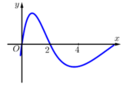
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
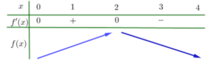
Từ bảng biến thiên, ta có nhận xét sau: ![]()
![]()
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
![]()
![]()
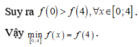
Cho hàm số \(y = f(u) = \sin u;\,\,u = g(x) = {x^2}\)
a) Bằng cách thay u bởi \({x^2}\) trong biểu thức \(\sin u\), hãy biểu thị giá trị của y theo biến số x.
b) Xác định hàm số \(y = f(g(x))\)
a: \(y=f\left(x^2\right)=sin\left(x^2\right)\)
b: \(y=f\left(g\left(x\right)\right)=f\left(x^2\right)=sinx^2\)
Cho hàm số f(x) xác định bởi ![]() . Giá trị f’(0) bằng
. Giá trị f’(0) bằng
A. 0
B. 2
C. 1
D. Không tồn tại.
Chọn D.
Ta có : 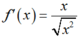
⇒ f’(x) không xác định tại x = 0
⇒ f’(0) không có đạo hàm tại x = 0.
Cho hàm số f(x) xác định trên R bởi f ( x ) = x 2 . Giá trị f ' (0) bằng
A. 0
B. 2
C. 1
D. không tồn tại
Chọn D
Ta có : f ' x = 1 2 x 2 . ( x 2 ) ' = x x 2
-> f '(x) không xác định tại x = 0
-> f ' (0) không có đạo hàm tại x= 0
Cho hàm số f(x) xác định trên bởi ![]() . Giá trị f’(-8) bằng:
. Giá trị f’(-8) bằng:
A. 1/12.
B. -1/12.
C. 1/6.
D. -1/6.
Cho hàm số f(x) xác định trên R bởi f(x)= 2 x 2 + 1 . Giá trị f ' (-1) bằng:
A. 2
B. 6
C. - 4
D. 3
Chọn C
Ta có : .f ' (x)=4x ⇒ f ' (-1)=-4