Chọn D.
Ta có : 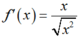
⇒ f’(x) không xác định tại x = 0
⇒ f’(0) không có đạo hàm tại x = 0.
Chọn D.
Ta có : 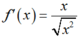
⇒ f’(x) không xác định tại x = 0
⇒ f’(0) không có đạo hàm tại x = 0.
Cho hàm số f(x) xác định bởi f ( x ) = x 2 + 1 - x x ( x ≠ 0 ) 0 ( x = 0 ) . Giá trị f’(0) bằng:
A. 0
B. 1
C. 1/2.
D. Không tồn tại.
Cho hàm số f(x) xác định trên R bởi f ( x ) = x 2 . Giá trị f ' (0) bằng
A. 0
B. 2
C. 1
D. không tồn tại
Cho hàm số f ( x ) = x 2 sin 1 x n ế u x ≠ 0 A n ế u x = 0
Xác định A để f(x) liên tục tại x = 0. Với giá trị A tìm được, hàm số có đạo hàm tại x = 0 không?
Cho hàm số f(x) xác định trên R bởi f(x)= 2 x 2 + 1 . Giá trị f ' (-1) bằng:
A. 2
B. 6
C. - 4
D. 3
Cho hàm số f(x) xác định trên R bởi f(x) = 2x2 + 1. Giá trị f’(-1) bằng:
A. 2.
B. 6.
C. -4.
D. 3.
Cho hàm số f(x) xác định trên R bởi f ( x ) = 2 x 2 + 1 . Giá trị f'(-1) bằng:
A. 2
B. 6
C. -4
D. 3
Cho hàm số y = f(x) xác định trên khoảng (a; +∞)
Chứng minh rằng nếu lim x → + ∞ f ( x ) = - ∞ thì luôn tồn tại ít nhất một số c thuộc (a; +∞) sao cho f(c) < 0
Cho hàm số f(x) xác định trên R\{1} bởi f ( x ) = 2 x x - 1 . Giá trị của bằng:
A. 1 2
B. - 1 2
C. -2
D. Không tồn tại
Cho hàm số f(x) xác định trên bởi ![]() . Giá trị f’(-8) bằng:
. Giá trị f’(-8) bằng:
A. 1/12.
B. -1/12.
C. 1/6.
D. -1/6.