Hãy viêt thuật toán sắp xếp N số hạng a 1 , a 2 , . . . . . , a n bằng cách tráo đổi
Những câu hỏi liên quan
Cho Dãy A gồmN=8.Dãy A gồm các số nguyênlà : 9 ,11, 3, 25, 1, 18,20, 2.Hãy sử dụng thuật toán sắp xếp tráo đổi( sắp xếp dãy A thành dãy không tăng)
Cách làm: Làm theo thứ tự các bước:
1.Xác định bài toán
2.Ý tưởng
3.Thuật toán( làm 1 trong 2 cách:Liệt kê và sơ đồ khối)
4.Ápdụng làm dãy số trên theo các lần duyệt như trong sách giáo khoa
#include <bits/stdc++.h>
using namespace std;
long long a[8],n,i,j;
int main()
{
n=8;
for (i=1; i<=n; i++) cin>>a[i];
for (i=1; i<=n-1; i++)
for (j=i+1; j<=n; j++)
if (a[i]<a[j]) swap(a[i],a[j]);
for (i=1; i<=n; i++) cout<<a[i]<<" ";
return 0;
}
Đúng 0
Bình luận (0)
29 tháng 12 2021 lúc 18:44
Mô phỏng thuật toán sắp xếp dãy số không giảm với N = 10 và dãy A : 6,1,5,3,7,8,10,7,12,4 . Hãy cho biết với lần duyệt thứ mấy để sắp xếp thành 1,3,4,5,6,7,7,8,10,12
#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
sort(a+1,a+n+1);
for (i=1; i<=n; i++) cout<<a[i]<<" ";
return 0;
}
Đúng 0
Bình luận (0)
SGK Cánh diều - Trang 125
18 tháng 7 2023 lúc 0:18
Em hãy thực hiện các công việc sau:
1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.
2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính.
1. Tính số lần lặp của vòng lặp bên trong của thuật toán sắp xếp chèn tuyến tính.
2. Tính số lần lặp của vòng lặp ngoài của thuật toán sắp xếp chèn tuyến tính.
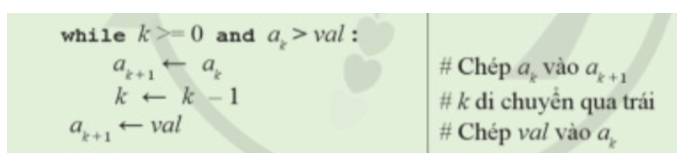
3. Ước lượng độ phức tạp thời gian của thuật toán sắp xếp chèn tuyến tính:
Vòng lặp for bên ngoài kiểm soát việc thực hiện đúng n-1 bước.
Vòng lặp while lồng bên trong thực hiện đồng thời cùng lúc hai việc a) và b) theo cách dịch chuyển dần từng bước sang trái, từ vị trí i tới vị trí k+1
Đúng 0
Bình luận (0)
Cho dạy B gồm 10 số nguyên tử a1 đến a10 gồm các số hạng 4, 71, 3, 40, 50, 9, 8, 7,1. Hãy sử dụng thuật toán sắp xếp bảng cách tráo đổi để sắp xếp dãy B thành dãy giảm
#include <bits/stdc++.h>
using namespace std;
long long b[10],i,j,n;
int main()
{
n=10;
for (i=1; i<=n; i++)
cin>>b[i];
for (i=1; i<=n-1; i++)
for (j=i+1;j<=n;j++)
if (b[i]<=b[j]) swap(b[i],b[j]);
for (i=1; i<=n; i++)
cout<<b[i]<<" ";
return 0;
}
Đúng 0
Bình luận (0)
Bạn có một hoán vị: một mảng a [a1, a2,…, an] gồm các số nguyên phân biệt từ 1 đến n. Độ dài của hoán vị n là số lẻ. Hãy xem xét thuật toán sắp xếp hoán vị theo thứ tự tăng dần sau đây. Thủ tục trợ giúp của thuật toán, f (i) , nhận một đối số duy nhất i (1≤i≤n − 1) và thực hiện như sau. Nếu ai ai + 1, giá trị của ai và ai + 1 được trao đổi. Nếu không, hoán vị không thay đổi. Thuật toán bao gồm các lần lặp, được đánh số bằng các số nguyên liên tiếp bắt đầu bằng 1 . Trên tôi -lặp lại thứ, thuật t...
Đọc tiếp
Bạn có một hoán vị: một mảng a = [a1, a2,…, an] gồm các số nguyên phân biệt từ 1 đến n. Độ dài của hoán vị n là số lẻ. Hãy xem xét thuật toán sắp xếp hoán vị theo thứ tự tăng dần sau đây. Thủ tục trợ giúp của thuật toán, f (i) , nhận một đối số duy nhất i (1≤i≤n − 1) và thực hiện như sau. Nếu ai> ai + 1, giá trị của ai và ai + 1 được trao đổi. Nếu không, hoán vị không thay đổi. Thuật toán bao gồm các lần lặp, được đánh số bằng các số nguyên liên tiếp bắt đầu bằng 1 . Trên tôi -lặp lại thứ, thuật toán thực hiện như sau:
nếu tôi là số lẻ, gọi f (1), f (3),…, f (n − 2) ;
nếu tôi là chẵn, gọi f (2), f (4),…, f (n − 1) .
Có thể chứng minh rằng sau một số lần lặp lại hữu hạn, hoán vị sẽ được sắp xếp theo thứ tự tăng dần. Sau bao nhiêu lần lặp lại điều này sẽ xảy ra lần đầu tiên?
Input:
Đầu vào Mỗi thử nghiệm chứa nhiều trường hợp thử nghiệm. Dòng đầu tiên chứa số lượng trường hợp thử nghiệm t (1≤t≤10 ^ 4 ). Sau đây là mô tả các trường hợp kiểm thử. Dòng đầu tiên của mỗi trường hợp kiểm tra chứa một số nguyên n (3≤n≤2⋅10 ^ 5−1; n là lẻ) - độ dài của hoán vị. Dòng thứ hai chứa n các số nguyên phân biệt a1, a2,…, an (1≤ai≤n ) - hoán vị chính nó. Đảm bảo rằng tổng của n trên tất cả các trường hợp thử nghiệm không vượt quá 2⋅10 ^ 5−1
Output:
. Đầu ra Đối với mỗi trường hợp thử nghiệm, in số lần lặp lại mà sau đó hoán vị sẽ được sắp xếp theo thứ tự tăng dần lần đầu tiên. Nếu hoán vị đã cho đã được sắp xếp, hãy in ra 0.
Input:
3
3
3 2 1
7
4 5 7 1 3 2 6
5
1 2 3 4 5
ouput:
3
5
0
Ghi chú Trong trường hợp thử nghiệm đầu tiên, hoán vị sẽ thay đổi như sau: sau 1 lần lặp -st: [2,3,1] ; sau 2 -nd lần lặp: [2,1,3] ; sau 3 -lặp lại thứ ba: [1,2,3] . Trong trường hợp thử nghiệm thứ hai, hoán vị sẽ thay đổi như sau: sau 1 lần lặp -st: [4,5,1,7,2,3,6] ; sau 2 -nd lần lặp: [4,1,5,2,7,3,6] ; sau 3 -lặp lại thứ ba: [1,4,2,5,3,7,6] ; sau 4 -lần lặp thứ: [1,2,4,3,5,6,7] ; sau 5 -lặp lại thứ: [1,2,3,4,5,6,7] . Trong trường hợp thử nghiệm thứ ba, hoán vị đã được sắp xếp và câu trả lời là 0 .
gốc: https://codeforces.com/problemset/problem/1558/F
Đúng 0
Bình luận (0)
10 tháng 4 2023 lúc 22:27
mô tả thuật toán và viết chương trình sắp xếp dãy số A gồm N phần tử(N được nhập từ bàn phím) sắp xếp theo thứ tự tăng dần
(pascal)
hãy phỏng thuật thuật toán sắp xếp tráo đổi với bộ dữ liệu sau n= 10 gồm { -1 5 90 82 -22 20 45 68 1 55}
Cho dãy A gồm các số sau: 4 7 9 1 6 3
Dựa vào thuật toán sắp xếp bằng tráo đổi để được 1 dãy tăng, hãy cho biết dãy thu được sau lần duyệt 1 và duyệt 2?
SGK Kết nối tri thức với cuộc sống - Trang 117
17 tháng 7 2023 lúc 18:23
Giả sử rằng mỗi phép tính đơn được thực hiện trong micro giây (1 us = một phần triệu giây). Hãy xác định giá trị lớn nhất của n trong các thuật toán tìm kiếm tuần tự, sắp xếp chèn và sắp xếp chọn nếu thời gian thực thi các thuật toán là 1 giây, 1 phút và 1 giờ?
1.Thuật toán tìm kiếm tuần tự:
- Độ phức tạp thời gian của thuật toán tìm kiếm tuần tự là O(n)
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = 1 giây * (106 us / phép tính) = 106
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = 1 phút * (60 giây / phút) * (106us / phép tính) = 6 * 107
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = 1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính) = 3.6 * 109
2.Thuật toán sắp xếp chèn:
- Độ phức tạp thời gian của thuật toán sắp xếp chèn là O(102
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = sqrt(1 giây * (106us / phép tính)) =103
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 6 * 104
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
3. Thuật toán sắp xếp chọn:
- Độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2)
- Giá trị lớn nhất của n là: n = sqrt(1 giây * (106us / phép tính)) = 1000.
Thời gian thực thi là 1 phút:
Giá trị lớn nhất của n là: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 60000.
Thời gian thực thi là 1 giờ:
Giá trị lớn nhất của n là: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
Đúng 1
Bình luận (0)