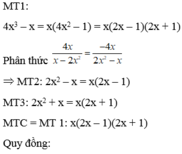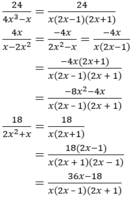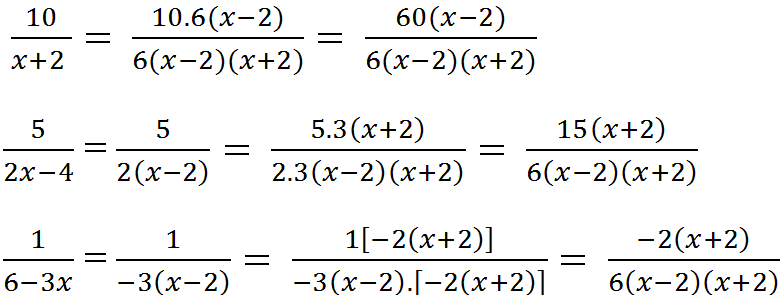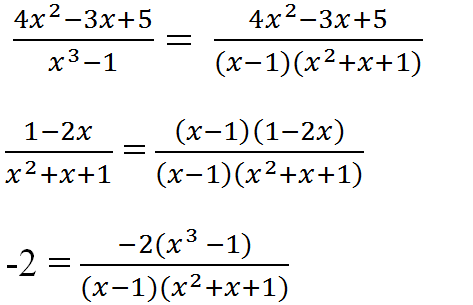Quy đồng mẫu thức các phân thức (có thể đổi dấu để tìm MTC cho thuận tiện). x - 1 2 x + 2 , x + 1 2 x - 2 , 1 1 - x 2

Những câu hỏi liên quan
Quy đồng mẫu thức các phân thức (có thể đổi dấu để tìm MTC cho thuận tiện).
24
1
x
3
-
x
,
4
x
x
-
2
x
2
,
18
2
x
2
+
x
Đọc tiếp
Quy đồng mẫu thức các phân thức (có thể đổi dấu để tìm MTC cho thuận tiện). 24 1 x 3 - x , 4 x x - 2 x 2 , 18 2 x 2 + x
Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu với một phân thức để tìm mẫu thức chung thuận tiện hơn)
a) \(\dfrac{4x^2-3x+5}{x^3-1},\dfrac{1-2x}{x^2+x+1},-2\)
b) \(\dfrac{10}{x+2},\dfrac{5}{2x-4},\dfrac{1}{6-3x}\)
a) Tìm MTC: x3 – 1 = (x – 1)(x2 + x + 1)
Nên MTC = (x – 1)(x2 + x + 1)
Nhân tử phụ:
(x3 – 1) : (x3 – 1) = 1
(x – 1)(x2 + x + 1) : (x2 + x + 1) = x – 1
(x – 1)(x2+ x + 1) : 1 = (x – 1)(x2 + x + 1)
Qui đồng:
b) Tìm MTC: x + 2
2x – 4 = 2(x – 2)
6 – 3x = 3(2 – x)
MTC = 6(x – 2)(x + 2)
Nhân tử phụ:
6(x – 2)(x + 2) : (x + 2) = 6(x – 2)
6(x – 2)(x + 2) : 2(x – 2) = 3(x + 2)
6(x – 2)(x + 2) : -3(x – 2) = -2(x + 2)
Qui đồng:
Đúng 0
Bình luận (1)
Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn):
\(\frac{4x^2-3x+5}{x^3-1}\), \(\frac{1-2x}{x^2+x+1}\)X ,\(-2\)
Tìm MTC: \(x^3-1=\left(x-1\right)\left(x^2+x+1\right)\)
Nên \(MTC=\left(x-1\right)\left(x^2+x+1\right)\)
Nhân tử phụ:
\(\left(x^3-1\right)\div\left(x^3-1\right)=1\)
\(\left(x-1\right)\left(x^2+x+1\right)\div\left(x^2+x+1\right)=x-1\)
\(\left(x-1\right)\left(x^2+x+1\right)\div1=\left(x-1\right)\left(x^2+x+1\right)\)
Quy đồng:
\(\frac{4x^2-3x+5}{x^3-1}=\frac{4x^2-3x+5}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(\frac{1-2x}{x^2+x+1}=\frac{\left(x-1\right)\left(1-2x\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(-2=\frac{-2\left(x^3-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
Đúng 0
Bình luận (0)
Qui đồng mẫu thức các phân thức sau (có thể áp dụng qui tắc đổi dấu với các phân thức để tìm mẫu thức chung thuận tiện hơn):
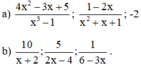
a) + Phân tích mẫu thức thành nhân tử để tìm nhân tử chung:
x3 – 1 = (x – 1)(x2 + x + 1)
x2 + x + 1 = x2 + x + 1
⇒ MTC = (x – 1)(x2 + x + 1) = x3 – 1
+ Nhân tử phụ : (Có thể bỏ qua bước này nếu đã quen)
(x3 – 1) : (x3 – 1) = 1
(x3 – 1) :( x2 + x + 1) = x - 1
(x3 – 1) : 1 = x3 – 1
+ Quy đồng :
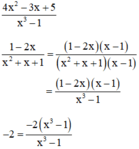
b) Ta có:
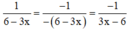
+ Phân tích mẫu thức thành nhân tử để tìm MTC
x + 2 = x + 2
2x – 4 = 2.(x – 2)
3x – 6 = 3.(x – 2)
⇒ MTC = 6.(x + 2)(x – 2)
+ Nhân tử phụ: (Có thể bỏ qua bước này nếu đã quen)
6(x + 2)(x – 2) : (x + 2) = 6(x – 2)
6(x + 2)(x – 2) : 2(x – 2) = 3(x + 2)
6(x + 2)(x – 2) : 3(x – 2) = 2(x + 2)
+ Quy đồng:
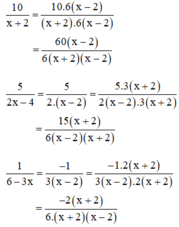
Đúng 0
Bình luận (0)
Đề bài: Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một phân thức để tìm mẫu thức chung thuận tiện hơn):
a) \(\frac{4x^2-3x+5}{x^3-1};\frac{1-2x}{x^2+x+1};-2\)
b) \(\frac{10}{x+2};\frac{5}{2x-4};\frac{1}{6-3x}\)
Làm ơn giải chi tiết nha, mình cảm ơn nhìu~~~
5. Quy đồng mẫu thức các phân thức sau (có thể áp dụng quy tắc đổi dấu đối với một số phân thức để tìm mẫu thức chung thuận tiện hơn):
a) \(\dfrac{4x^2-3x+5}{x^3-1},\dfrac{1-2x}{x^2+x+1},x-2\) b) \(\dfrac{10}{x+2},\dfrac{5}{2x-4},\dfrac{1}{6-3x}\)
a) Tìm MTC: x3 – 1 = (x – 1)(x2 + x + 1)
Nên MTC = (x – 1)(x2 + x + 1)
Nhân tử phụ:
(x3 – 1) : (x3 – 1) = 1
(x – 1)(x2 + x + 1) : (x2 + x + 1) = x – 1
(x – 1)(x2+ x + 1) : 1 = (x – 1)(x2 + x + 1)
Qui đồng:
b) Tìm MTC: x + 2
2x – 4 = 2(x – 2)
6 – 3x = 3(2 – x)
MTC = 6(x – 2)(x + 2)
Nhân tử phụ:
6(x – 2)(x + 2) : (x + 2) = 6(x – 2)
6(x – 2)(x + 2) : 2(x – 2) = 3(x + 2)
6(x – 2)(x + 2) : -3(x – 2) = -2(x + 2)
Qui đồng:
Đúng 0
Bình luận (0)
Đọc tiếp
Xem thêm câu trả lời
quy đồng mẫu thức các phân thức a) dfrac{1}{2x^3y}:dfrac{2}{3xy^2z^3}:dfrac{5}{4yz}b) dfrac{x+1}{10x^3-40x} và dfrac{5}{8x^3+16x^2}bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thứcdfrac{2-x}{3x-3x^2} và dfrac{x^2-2}{4x^5-4x^2}giúp mik với mik cần gấp
Đọc tiếp
quy đồng mẫu thức các phân thức a) \(\dfrac{1}{2x^3y}\):\(\dfrac{2}{3xy^2z^3}\):\(\dfrac{5}{4yz}\)
b) \(\dfrac{x+1}{10x^3-40x}\) và \(\dfrac{5}{8x^3+16x^2}\)
bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thức
\(\dfrac{2-x}{3x-3x^2}\) và \(\dfrac{x^2-2}{4x^5-4x^2}\)
giúp mik với mik cần gấp
quy đồng mẫu thức các phân thức a) dfrac{1}{2x^3y}: dfrac{2}{3xy^2z^3}:dfrac{5}{4yz}b) dfrac{x+1}{10x^3-40x} và dfrac{5}{8x^3+16x^2}bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thứcdfrac{2-x}{3x-3x^2} và dfrac{x^2-2}{4x^5-4x^2}
Đọc tiếp
quy đồng mẫu thức các phân thức a) \(\dfrac{1}{2x^3y}:\) \(\dfrac{2}{3xy^2z^3}\):\(\dfrac{5}{4yz}\)
b) \(\dfrac{x+1}{10x^3-40x}\) và \(\dfrac{5}{8x^3+16x^2}\)
bài 2 áp dụng quy tắc đổi dấu hãy quy đồng mẫu thức các phân thức
\(\dfrac{2-x}{3x-3x^2}\) và \(\dfrac{x^2-2}{4x^5-4x^2}\)
Bài 2:
a: \(\dfrac{1}{2x^3y}=\dfrac{6yz^3}{12x^3y^2z^3}\)
\(\dfrac{2}{3xy^2z^3}=\dfrac{2\cdot4x^2}{12x^3y^2z^3}=\dfrac{8x^2}{12x^3y^2z^3}\)
Đúng 0
Bình luận (0)