Cho bốn điểm A, B, C và D không đồng phẳng. Gọi G A , G B , G C , G D lần lượt là trọng tâm của các tam giác BCD, CDA, ADB, ACB. Chứng minh rằng A G A , B G B , C G C , D G D đồng qui.

Những câu hỏi liên quan
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi I, K lần lượt là trung điểm của AD và BC.
a) Tìm giao tuyến của hai mặt phẳng (IBC) và (KAD).
b) Gọi M và N là hai điểm lần lượt lấy trên hai đoạn thẳng AB và AC. Tìm giao tuyến của hai mặt phẳng (IBC) và (DMN).
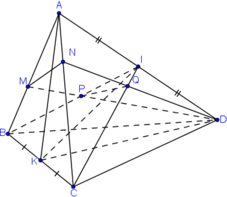
a) Tìm giao tuyến của mp(IBC) và mp(KAD).
Ta có:
K ∈ BC ⇒ K ∈ (IBC) ⇒ K ∈ (IBC) ∩ (KAD)
I ∈ AD ⇒ I ∈ (KAD) ⇒ I ∈ (IBC) ∩ (KAD)
Vậy KI = (IBC) ∩ (KAD)
b) Trong mp(ABD) gọi BI ∩ DM = P
⇒ P ∈ (IBC) ∩ (DMN)
Trong mặt phẳng (ACD) gọi CI ∩ DN = Q
⇒ Q ∈ (IBC) ∩ (DMN)
Vậy (IBC) ∩ (DMN) = PQ.
Đúng 1
Bình luận (0)
Cho bốn điểm A, B, C và D không đồng phẳng. Gọi M và N lần lượt là trung điểm của các đoạn thẳng AC và BC. Trên đoạn BD lấy điểm P sao cho BP = 2PD.
a) Tìm giao điểm của đường thẳng CD và mặt phẳng (MNP).
b) Tìm giao tuyến của hai mặt phẳng (MNP) và (ACD).
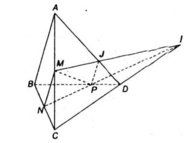
a) Ta có:
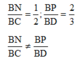
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I.
I ∈ NP ⇒ I ∈ (MNP).
Mà I ∈ CD
Vậy I ∈ CD ∩ (MNP)
b) Trong mặt phẳng (ACD) thì AD và MI cắt nhau tại điểm J:
J ∈ AD ⇒ J ∈ (ACD)
J ∈ MI ⇒ J ∈ (MNP)
Vậy J là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MJ = (ACD) ∩ (MNP).
Đúng 0
Bình luận (0)
Quan sát hình hộp chữ nhật (h.102)

a) Các cặp mặt phẳng nào song song với nhau ?
b) Các điểm D, H, G và C có cùng thuộc một mặt phẳng không ?
c) Các điểm D, H, G và F có cùng thuộc một mặt phẳng không ?
d) Câu hỏi tương tự như câu b), c) đối với các điểm A, B, G và H ?
a: \(mp\left(EFGH\right);mp\left(ABCD\right)\)
\(mp\left(ABFE\right);mp\left(CDHG\right)\)
\(mp\left(ADHE\right);mp\left(BCGF\right)\)
b: Các điểm D,H,G,C cùng thuộc mặt phẳng CDHG
c: Các điểm D,H,G,F không thuộc cùng một mặt phẳng
d: A,B,G,H cùng thuộc mặt phẳng ABGH
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).(c) Lấy một điểm K trên đoạn SE và gọi C SC ∩KB, DSD ∩KA. Chứng minh rằng hai giao điểm của AC và BD thuộc đườn...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB là đáy lớn. Gọi M là trung điểm của đoạn AB, E là giao điểm của hai cạnh của hình thang ABCD và G là trọng tâm của tam giác ECD.
(a) Chứng minh rằng bốn điểm S, E, M, G cùng thuộc một mặt phẳng (α) và mặt phẳng này cắt cả hai mặt phẳng (SAC) và (SBD) theo cùng một giao tuyến d.
(b) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC).
(c) Lấy một điểm K trên đoạn SE và gọi C' = SC ∩KB, D'=SD ∩KA. Chứng minh rằng hai giao điểm của AC' và BD' thuộc đường thẳng d nói trên.
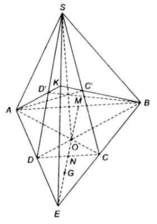
a) Gọi N là giao điểm của EM và CD
Vì M là trung điểm của AB nên N là trung điểm của CD (do ABCD là hình thang)
⇒ EN đi qua G
⇒ S, E, M, G ∈ (α) = (SEM)
Gọi O là giao điểm của AC và BD
Ta có (α) ∩ (SAC) = SO
và (α) ∩ (SBD) = SO = d
b) Ta có: (SAD) ∩ (SBC) = SE
c) Gọi O' = AC' ∩ BD'
Ta có AC' ⊂ (SAC), BD' ⊂ (SBD)
⇒ O' ∈ SO = d = (SAC) ∩ (SBD)
Đúng 0
Bình luận (0)
Cho hai điểm A, B nằm trong nửa mặt phẳng bờ là đường thẳng d. Gọi AH, BK là các đường vuông góc kẻ từ A, B đến d. Gọi C là điểm bất kì nằm giữa H và K, A’ đối xứng với A qua d. Giả sử góc ACH = góc BCK. CMR: Khi đó A’, C, B thẳng hàng
Xét ΔCAA' có
CH vừa là đường cao, vừa là đường trung tuyến
nên ΔCA'A cân tại C
=>CH là phân giác của góc ACA'
=>góc A'CH=góc BCK
=>góc A'CH+góc HCB=180 độ
=>A',C,B thẳng hàng
Đúng 0
Bình luận (0)
Cho góc xOy khác góc bẹp. Trên tia Ox lấy ba điểm A, B, C không trùng O. Trên tia Oy lấy bốn điểm D, E, G, H không trùng O. Có bao nhiêu tam giác mà đỉnh là ba trong tám điểm O, A, B, C, D, E, G, H.
Quan sát hình vẽ và điền Đ(đúng) hoặc S(sai) và ô vuông
a. B, C là các điểm nằm trong mặt phẳng (P).
b, Mặt phẳng (P) chứa đựờng thắng AB
c. Đường thẳng l cắt AB ở điểm B
d. A,B,G là ba điểm cùng nằm trên một mặt phẳng
e. B,F và D là ba điểm thẳng hàng
f. B,C,E và D là bốn điểm cùng nằm trên một mặt phẳng
Đọc tiếp
Quan sát hình vẽ và điền Đ(đúng) hoặc S(sai) và ô vuông
| a. B, C là các điểm nằm trong mặt phẳng (P). | |
| b, Mặt phẳng (P) chứa đựờng thắng AB | |
| c. Đường thẳng l cắt AB ở điểm B | |
| d. A,B,G là ba điểm cùng nằm trên một mặt phẳng | |
| e. B,F và D là ba điểm thẳng hàng | |
| f. B,C,E và D là bốn điểm cùng nằm trên một mặt phẳng |
| a. B, C là các điểm nằm trong mặt phẳng (P). | Đ |
| b, Mặt phẳng (P) chứa đựờng thắng AB | S |
| c. Đường thẳng l cắt AB ở điểm B | S |
| d. A,B,G là ba điểm cùng nằm trên một mặt phẳng | Đ |
| e. B,F và D là ba điểm thẳng hàng | S |
| f. B,C,E và D là bốn điểm cùng nằm trên một mặt phẳng | Đ |
Đúng 0
Bình luận (0)
Trong không gian Oxyz , cho điểm
G
-
1
;
2
;
-
1
.
Mặt phẳng (a) đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng (a) ? A.
N
-
3
;
4...
Đọc tiếp
Trong không gian Oxyz , cho điểm G - 1 ; 2 ; - 1 . Mặt phẳng (a) đi qua G và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho G là trọng tâm của DABC . Điểm nào sau đây thuộc mặt phẳng (a) ?
A. N - 3 ; 4 ; 2
B. P - 3 ; - 4 ; 2
C. Q 3 ; 4 ; 2
D. M 3 ; 4 ; - 2
cho góc xoy khác góc bẹt. trên tia õ lấy ba điểm A,B,C không trùng O. trên tia oy lấy bốn điểm D,E,G,H không trùng o. có bao nhiêu tam giác mà các đỉnh là ba trong tám điểm O,A,B,C,D,E,G,H









