Cho hình 4, biết A ^ 1 = B ^ 1 , C ^ 1 = C ^ 2 . Chứng minh rằng m ⊥ b .
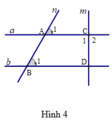
xem hình và cho biết khẳng định nào chứng tỏ a//b
1. A1=B2
2. A4=B3
3. A2=B3
4. A1=B4
5. A3=B2
6. A4=B1
7. A1+B3=180
8.A4+B2=180
Cho hình vẽ bên cho biết a // b và A ^ 1 − B ^ 2 = 70 0 . Hãy tính A ^ 3 và B ^ 4
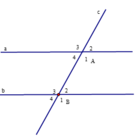
+) Vì a // b nên A ^ 1 + B ^ 2 = 180 ∘ (cặp góc trong cùng phía)
Mặt khác A ^ 1 − B ^ 2 = 70 0
⇒ A ^ 1 = 180 ∘ + 70 ∘ : 2 = 125 ∘ và B ^ 2 = 180 ∘ − 125 ∘ = 55 ∘
+) Ta có A ^ 3 = A ^ 1 (hai góc đối đỉnh) mà A ^ 1 = 125 ∘
⇒ A ^ 3 = 125 ∘
Ta có B ^ 2 = B ^ 4 (hai góc đối đỉnh) mà B ^ 2 = 55 ∘
⇒ B ^ 4 = 55 ∘
Cho hình hộp ABCD.A'B'C'D' biết A(1; 0; 1), B(2; 1; 2), D(1; -1; 1), C'(4; 5; -5). Tính tọa độ các đỉnh còn lại của hình hộp.
Với hình vẽ bên . Cho biết N^1+N^4+M^1=228 độ và N^1=4/11 N^4. Hãy giải thích vì sao a song song với b
Cho hình vẽ, cho biết a // b và b ⊥ c
a)Đường thẳng a có vuông góc với đường thẳng c không ? vì sao?
b)Cho đường thẳng d cắt hai đường thẳng a và b tại C và D. Cho biết D4 = 65 . Tính số đo các góc D2 C3 C4
a, Vì a//b và b⊥c nên a⊥c
b, Ta có \(\widehat{D_2}=\widehat{D_4}=65^0\) (đối đỉnh)
Vì a//b nên \(\widehat{C_4}=\widehat{D_2}=65^0\) (so le trong)
\(\widehat{C_3}+\widehat{C_4}=180^0\) (kề bù)
Hay \(\widehat{C_3}=180^0-65^0=115^0\)
cho hình vuông abcd và 1/4 hình tròn bán kính DA.Tính diện tích phần tô đậm,biết cạnh hình vuông là 4cm.
Như này chưa rõ được em
1.Thực hiện phép tính
a) 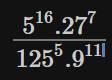
b)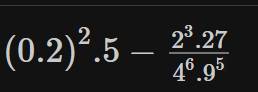
c)
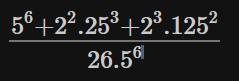
2.Tìm số hữu tỉ a, biết rằng lấy a nhân với 1/2 rồi cộng với 3/4, sau đó chia kết quả cho -1/4 thì đc số -15/4
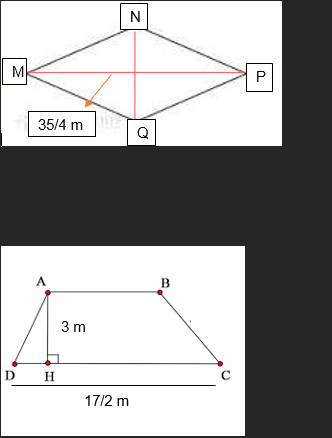
3.a) Tính diện tích hình thang ABCD có các kích thước như hình sau:
b) Hình thoi MNPQ có diện tích bằng diện tích hình thang ABCD ở câu a, đường chéo MP=35/4.Tính độ dài NQ
Bài 1:
a) \(\dfrac{5^{16}\cdot27^7}{125^5\cdot9^{11}}\)
\(=\dfrac{5^{16}\cdot\left(3^3\right)^7}{\left(5^3\right)^5\cdot\left(3^2\right)^{11}}\)
\(=\dfrac{5^{16}\cdot3^{21}}{5^{15}\cdot3^{22}}\)
\(=\dfrac{5}{3}\)
b) \(\left(0,2\right)^2\cdot5-\dfrac{2^3\cdot27}{4^6\cdot9^5}\)
\(=0,2\cdot5\cdot0,2-\dfrac{2^3\cdot3^3}{\left(2^2\right)^6\cdot\left(3^2\right)^5}\)
\(=\dfrac{1}{5}-\dfrac{2^3\cdot3^3}{2^{12}\cdot3^{10}}\)
\(=\dfrac{1}{5}-\dfrac{1}{2^9\cdot3^7}\)
\(=\dfrac{2^9\cdot3^7}{2^9\cdot3^7\cdot5}-\dfrac{5}{2^9\cdot3^7\cdot5}\)
\(=\dfrac{2^9\cdot3^7-5}{2^9\cdot3^7\cdot5}\)
c) \(\dfrac{5^6+2^2\cdot25^3+2^3\cdot125^2}{26\cdot5^6}\)
\(=\dfrac{5^6\cdot\left(1+2^2+2^3\right)}{26\cdot5^6}\)
\(=\dfrac{1+2^2+2^3}{26}\)
\(=\dfrac{1+4+8}{26}\)
\(=\dfrac{13}{26}\)
\(=\dfrac{1}{2}\)
Bài 2:
Theo đề ta có:
\(\left(a\cdot\dfrac{1}{2}+\dfrac{3}{4}\right):-\dfrac{1}{4}=-\dfrac{15}{4}\)
\(\Rightarrow\left(a\cdot\dfrac{1}{2}+\dfrac{3}{4}\right)=-\dfrac{15}{4}\cdot-\dfrac{1}{4}\)
\(\Rightarrow a\cdot\dfrac{1}{2}+\dfrac{3}{4}=\dfrac{15}{16}\)
\(\Rightarrow a\cdot\dfrac{1}{2}=\dfrac{15}{16}-\dfrac{3}{4}\)
\(\Rightarrow a\cdot\dfrac{1}{2}=\dfrac{3}{16}\)
\(\Rightarrow a=\dfrac{3}{16}:\dfrac{1}{2}\)
\(\Rightarrow a=\dfrac{3}{8}\)
1:
a: \(=\dfrac{5^{16}\cdot3^{21}}{3^{22}\cdot5^{15}}=\dfrac{1}{3}\cdot5=\dfrac{5}{3}\)
b: \(=0.04\cdot5-\dfrac{2^3\cdot3^3}{3^6\cdot2^{12}}\)
\(=0.2-\dfrac{1}{3^3\cdot2^9}=\dfrac{1}{5}-\dfrac{1}{3^3\cdot2^9}=\dfrac{3^3\cdot2^9-5}{5\cdot3^3\cdot2^9}\)
c: \(=\dfrac{5^6+4\cdot5^6+2^3\cdot5^6}{26\cdot5^6}=\dfrac{1+4+8}{26}=\dfrac{13}{26}=\dfrac{1}{2}\)
2:
Theo đề, ta có:
\(\left(a\cdot\dfrac{1}{2}+\dfrac{3}{4}\right):\dfrac{-1}{4}=\dfrac{-15}{4}\)
=>\(\dfrac{1}{2}a+\dfrac{3}{4}=\dfrac{15}{16}\)
=>1/2a=15/16-12/16=3/16
=>a=3/8
Bài 4:Cho hình vẽ, biết a\(\perp\)MP tại M, \(b\perp NQ\) tại Q, \(\widehat{N_1}\)=\(65^O\).
a) Chứng tỏ a//b.
b) Tính \(\widehat{M_1}\)=?
ta có : a \(\perp\) P và b \(\perp\) Q \(\Rightarrow\)a//b
M1 và N1 là cặp góc trong cùng phía bù nhau
\(\Rightarrow\)M1= \(^{180^0}\)- N1= 180- \(65^0\)= 115
Cho hình tam giác abc. Trên BC lấy điểm M sao cho BM = 1/4 BC, nối A vói điểm AM lấy N sao cho NM = 1/3 AM. Nối B với N, biết diện tích hình tam giác BMN = 4cm2. Tính S hình tam giác ABC.