Hàm nghịch biến trên R khi:

\(\left\{{}\begin{matrix}a< 0\\a+5\ge0\end{matrix}\right.\) \(\Rightarrow-5\le a< 0\)

Lời giải:

ĐK: $m\geq -5$

Để hàm nghịch biến trên $R$ thì $m<0$

Vậy $-5\leq m< 0$. Vì $m$ nguyên nên $m\in\left\{-5;-4;-3;-2;-1\right\}$

Chọn D

Cách1:

Ta có: .

Vậy

.

Đặt .

Vậy .

Ta có: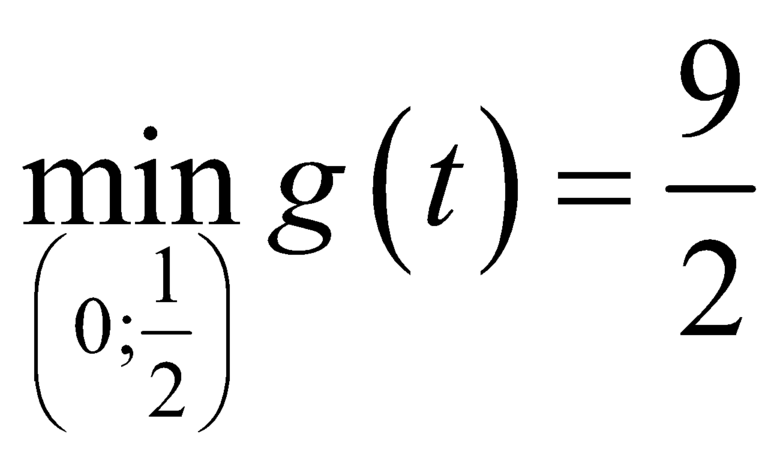. Vậy .

Chọn A.

Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx

Hàm số nghịch biến trên R

Trường hợp 1: m= -1/ 2 ; ta có  0 ≤ 7 2   ∀ x ∈ ℝ

Vậy hàm số luôn nghịch biến trên R.

Trường hợp 2: m< -1/ 2 ; ta có

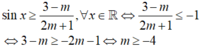
Trường hợp 3:m > -1/2 ; ta có:

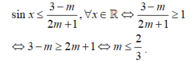
Vậy  - 4 ≤ m ≤ 2 3

a: Vì \(a=1-\sqrt5<0\)

nên hàm số \(y=\left(1-\sqrt5\right)x-1\) nghịch biến trên R

b: Thay \(x=1+\sqrt5\) vào \(y=\left(1-\sqrt5\right)x-1\) , ta được:

\(y=\left(1-\sqrt5\right)\left(1+\sqrt5\right)-1\)

=1-5-1

=-5

c: Đặt \(y=\sqrt5\)

=>\(\left(1-\sqrt5\right)x-1=\sqrt5\)

=>\(\left(1-\sqrt5\right)x=\sqrt5+1\)

=>\(x=-\frac{\sqrt5+1}{\sqrt5-1}=-\frac{\left(\sqrt5+1\right)^2}{\left(\sqrt5-1\right)\left(\sqrt5+1\right)}=-\frac{6+2\sqrt5}{5-1}=-\frac{6+2\sqrt5}{4}=-\frac{3+\sqrt5}{2}\)