7). Đi qua điểm P(-5;4) và song song với trục hoành

Những câu hỏi liên quan
Tìm pt đườg thẳg đi qua điểm A(7/3;-5/2) và đi qua gđ 2 đườg thẳgd1:y=3x-5 và d2:y=-x+4
Lời giải:
Gọi PTĐT cần tìm có dạng $(\Delta)$: $y=ax+b$ $(a,b\in\mathbb{R}$)
PT hoành độ giao điểm của 2 đường thẳng $(d_1); (d_2)$ là:
\(y=3x-5=-x+4\)
\(\Rightarrow x=\frac{9}{4}\Rightarrow y=\frac{7}{4}\)
Vậy giao điểm của $(d_1); (d_2)$ là $B(\frac{9}{4}, \frac{7}{4})$
Vì $A,B\in (\Delta)$ nên:
\(\left\{\begin{matrix} \frac{-5}{2}=a.\frac{7}{3}+b\\ \frac{7}{4}=a.\frac{9}{4}+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=-51\\ b=\frac{233}{2}\end{matrix}\right.\)
\(\Rightarrow (\Delta): y=-51x+\frac{233}{2}\)
Đúng 0
Bình luận (0)
Tìm giao điểm của hai đường thẳng: (
d
1
): 5x – 2y c và (
d
2
): x + by 2, biết rằng (
d
1
) đi qua điểm A(5; -1) và (
d
2
) đi qua điểm B(-7; 3).
Đọc tiếp
Tìm giao điểm của hai đường thẳng: ( d 1 ): 5x – 2y = c và ( d 2 ): x + by = 2, biết rằng ( d 1 ) đi qua điểm A(5; -1) và ( d 2 ) đi qua điểm B(-7; 3).
*Đường thẳng ( d 1 ): 5x – 2y = c đi qua điểm A(5; -1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.
Ta có: 5.5 – 2.(-1) = c ⇔ 25 + 2 = c ⇔ c = 27
Phương trình đường thẳng ( d 1 ): 5x – 2y = 27
*Đường thẳng ( d 2 ): x + by = 2 đi qua điểm B(-7; 3) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.
Ta có: -7 + 3b = 2 ⇔ 3b = 9 ⇔ b = 3
Phương trình đường thẳng ( d 2 ): x + 3y = 2
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình:![]()
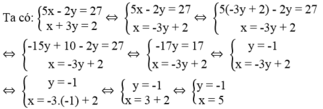
Vậy tọa độ giao điểm của ( d 1 ) và ( d 2 ) là (5; -1).
Đúng 0
Bình luận (0)
chứng minh rằng
a) Họ đường thẳng k(x+3)-7-y=0 luôn đi qua điểm cố định với mọi k
b) Họ đường thẳng (m+2)x+(m-3)y-m+8=0 luôn đi qua điểm cố định với mọi m
c) Họ đường thẳng y=(2-k)x+k-5 luôn đi qua điểm cố định với mọi k
a/ Gọi điểm cố định \(M\left(x_0;y_0\right)\)
Khi đó đường thẳng y = k(x+3)-7 đi qua M , tức \(k\left(x_0+3\right)-7-y_0=0\)
Vì đường thẳng y = k(x+3)-7 luôn đi qua M nên \(\hept{\begin{cases}x_0+3=0\\-y_0-7=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=-3\\y_0=-7\end{cases}}\)
Vậy đường thẳng đã cho luôn đi qua điểm M(-3;-7)
b/ Gọi điểm cố định là \(N\left(x_0;y_0\right)\)
Vì họ đường thẳng (m+2)x + (m-3)y -m+8 = 0 luôn đi qua N nên :
\(\left(m+2\right).x_0+\left(m-3\right).y_0-m+8=0\)
\(\Leftrightarrow m\left(x_0+y_0-1\right)+\left(2x_0-3y_0+8\right)=0\)
Ta có \(\hept{\begin{cases}x_0+y_0-1=0\\2x_0-3y_0+8=0\end{cases}}\) \(\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=2\end{cases}}\)
Vậy điểm cố định N(-1;2)
Câu còn lại bạn làm tương tự nhé ^^
Đúng 0
Bình luận (0)
c/ Đơn giản thôi mà =)
Ta cũng gọi điểm cố định đó là \(M\left(x_0;y_0\right)\)
Vì họ đường thẳng y=(2-k)x+k-5 đi qua M nên :
\(y_0=\left(2-k\right)x_0+k-5\Leftrightarrow k\left(1-x_0\right)+\left(2x_0-y_0-5\right)=0\)
Ta có \(\hept{\begin{cases}1-x_0=0\\2x_0-y_0-5=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=1\\y_0=-3\end{cases}}\)
Vậy điểm cố định là M(1;-3)
Đúng 1
Bình luận (0)
Câu 7:
Cho 5 điểm trong đó không có 3 điểm nào thẳng hàng. Số tất cả các đường thẳng đi qua 2 trong 5 điểm đã cho là
Viết PT tổng quát của đưoqngf thẳng d trong mỗi trường hợp sau 1: d đi qua điểm M (7;0) và song song với denta🔺️ : 2x+3y-140
2: d đi qua điểm M (0;3) và song song với trục 0x
3 : d đi qua gốc tọa độ O và song song với đường thẳng denta :
{x1-2t
Y3+4t ( hai pt này chung dấu ngoặc nhé )
4: d đi qua điểm M(1;-4) và vuông góc với đt denta :x/5 y-4/2
5: d đi qua điểm M (4;3) và vuông góc với trục Oy
6: d đi qua điểm M (-2;0) và vuông góc với đường phân giác của góc phần tư thứ 2 và thứ 4 củ...
Đọc tiếp
Viết PT tổng quát của đưoqngf thẳng d trong mỗi trường hợp sau 1: d đi qua điểm M (7;0) và song song với denta🔺️ : 2x+3y-14=0
2: d đi qua điểm M (0;3) và song song với trục 0x
3 : d đi qua gốc tọa độ O và song song với đường thẳng denta :
{x=1-2t
Y=3+4t ( hai pt này chung dấu ngoặc nhé )
4: d đi qua điểm M(1;-4) và vuông góc với đt denta :x/5 =y-4/2
5: d đi qua điểm M (4;3) và vuông góc với trục Oy
6: d đi qua điểm M (-2;0) và vuông góc với đường phân giác của góc phần tư thứ 2 và thứ 4 của hệ trục tọa độ Oxy
7: d đi qua giao điểm của d1 : 3x-5y+2=0 ,
d2 :5x-2y+4=0, d song song d3: 2x-y+4=0
8: d đi qua giao điểm của d1 :3x-2y+5=0 , d2 : 2x+4y-7=0 , d vuông góc d3: 4x-3y+5=0
Xác định giá trị m, k biết:
a. Đồ thị hàm số \(y=3x+m\)đi qua điểm (2; 7).
b Đồ thị hàm số \(y=kx+5\)đi qua điểm (2;11).
Do đồ thị hàm số đi qua điểm ( 2;7 )
\(\Rightarrow x=2;y=7\)
Thay vào hàm số \(y=3x+m\) ta được :
\(\Rightarrow7=3.2+m\)
\(\Rightarrow m=1\)
b, do đồ thị hàm số đi qua điểm ( 2 ; 11 )
\(\Rightarrow x=2;y=11\)
Thay vào hàm số \(y=kx+5\) ta được :
\(11=2k+5\)
\(\Rightarrow k=3\)
k mk nha
Đúng 0
Bình luận (0)
Trong các cách sau, có bao nhiêu cách để xác định một mặt phẳng 1. Đi qua 3 điểm phân biệt 2. Đi qua 1 điểm và chứa 1 đường thẳng không đi qua điểm đó 3. Đi qua 2 đường thẳng bất kì 4. Đi qua đường thẳng (d1) và song song với đường thẳng (d2) cho trước, sao cho d1 và d2 không cắt nhau 5. Song song với 2 đường thẳng cắt nhau 6. Song song với 2 đường thẳng chéo nhau 7. Đi qua 1 điểm và song song với một đường thẳng cho trước 8. Đi qua 1 điểm và song song với một m...
Đọc tiếp
Trong các cách sau, có bao nhiêu cách để xác định một mặt phẳng
1. Đi qua 3 điểm phân biệt
2. Đi qua 1 điểm và chứa 1 đường thẳng không đi qua điểm đó
3. Đi qua 2 đường thẳng bất kì
4. Đi qua đường thẳng (d1) và song song với đường thẳng (d2) cho trước, sao cho d1 và d2 không cắt nhau
5. Song song với 2 đường thẳng cắt nhau
6. Song song với 2 đường thẳng chéo nhau
7. Đi qua 1 điểm và song song với một đường thẳng cho trước
8. Đi qua 1 điểm và song song với một mặt phẳng cho trước
A. 2
B. 3
C. 4
D. 5
Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy
Đúng 0
Bình luận (0)
Cho 3 điểm A ( 0; -8 ) , B ( 5/2 ; 2 ) , C ( 1; 7 ) và đường thẳng (d1) có phương trình 3x + 2y = -1
a, Viết phương trình đường thẳng (d2) đi qua hai điểm A và B
b, Viết phương trình đường thẳng (d3) đi qua điểm C và song song với (d1)
1 Tìm n thuộc Z
a,n2-7 là bội của n+3
2 Cho 5 điểm
a . Có bao nhiêu đoạn thẳng qua 5 điểm đó
b. Cho đường thẳng a ko đi qua bất kì điểm nào trong 5 điểm đó. Chứng tỏ a ko thể cắt đc 5 đoạn thẳng đc tạo thành 5 điển đã cho
\(n^2-7=\)\(n^2-9+2=\left(n-3\right)\left(n+3\right)+2\)
Vì \(\left(n-3\right)\left(n+3\right)\) chia hết cho n+3
\(\Rightarrow2\)chia hết cho n+3
\(\Rightarrow n+3\in\left(-1;1;-2;2\right)\)
còn lại tự làm
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho 2 điểm A(-2;4;-5); B(1; -7; 0)
Viết phương trình chính tắc của đường thẳng đi qua 2 điểm A,B
\(\overrightarrow{AB}=\left(1--2,-7-4,0--5\right)=\left(3,-11,5\right)\)
Đi qua \(A\left(-2,4,-5\right)\)
Phương trình chính tắc :
\(\dfrac{x+2}{3}=\dfrac{y-4}{-11}=\dfrac{z+5}{5}\)
Đúng 1
Bình luận (0)

















