Ta tìm đỉnh của parabol:

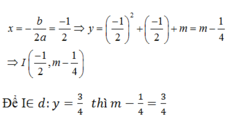
Suy ra m=1.

Chọn D.

a: Thay x=1 và y=3 vào (d), ta được:

m+3-m=3

=>3=3(luôn đúng)

b: PTHĐGĐ là:

x^2-mx-3+m=0

=>x^2-mx+m-3=0

Để (d) cắt (P) tại hai điểm phân biệt thì m-3<0

=>m<3

A thuộc y=x+2 nên A(x;x+2)

Theo đề, ta có:

\(\left\{{}\begin{matrix}x=\dfrac{2m}{2}=m\\x+2=-\dfrac{\left(2m\right)^2-4\left(m+3\right)}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m\\x+2=-\dfrac{4m^2-4m-12}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=m\\x+2=-m^2+m+3\end{matrix}\right.\Leftrightarrow-m^2+m+3-2=m\)

=>-m^2+m+1-m=0

=>1-m^2=0

=>m=1

a: Thay x=3 và y=0 vào (1), ta được:

\(6-3m=0\)

hay m=2

Đỉnh parabol : \(I\left(1;-m^2-m-2\right)\) nằm trên đt y = x - 3 \(\Leftrightarrow x=1;y=-m^2-m-2\) t/m ct h/s :

\(-m^2-m-2=1-3\)

\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\end{matrix}\right.\)(loại m = 0)

a) Khi \(m=1\) \(\Rightarrow\left(d\right):y=2x+8\)

Xét phương trình hoành độ giao điểm

  \(x^2=2x+8\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)

+) Với \(x=4\Rightarrow y=16\)

+) Với \(x=-2\Rightarrow y=4\)

  Vậy khi \(m=1\) thì (P) cắt (d) tại 2 điểm phân biệt \(\left(4;16\right)\) và \(\left(-2;4\right)\)

b) Xét phương trình hoành độ giao điểm

  \(x^2-2x+m^2-9=0\)  (*)

Ta có: \(\Delta'=10-m^2\) 

Để (P) cắt (d) \(\Leftrightarrow\) Phương trình (*) có 2 nghiệm phân biệt 

\(\Leftrightarrow\Delta'=10-m^2>0\) \(\Leftrightarrow-\sqrt{10}< m< \sqrt{10}\)

Theo đề: (P) cắt (d) tại 2 điểm nằm về 2 phía của trục tung

\(\Leftrightarrow\) Phương trình (*) có 2 nghiệm trái dấu

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1x_2< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}10-m^2>0\\m^2-9< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{10}< m< \sqrt{10}\\-3< m< 3\end{matrix}\right.\) \(\Leftrightarrow-3< m< 3\)

  Vậy ...