Ta tìm đỉnh của parabol:
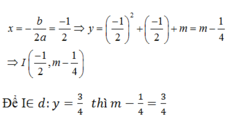
Suy ra m=1.
Chọn D.
Ta tìm đỉnh của parabol:
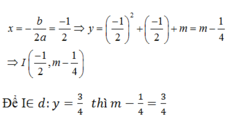
Suy ra m=1.
Chọn D.
Đỉnh của parabol y = x 2 + x + m nằm trên đường thẳng y = 3 4 nếu m bằng:
A. Một số tùy ý
B. 3
C. 5
D. 1
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
Cho A(m;3) B(2;1) C(-4;5) a) tìm điều kiện của m để A,B,C là 3 đỉnh của một tam giác b) tìm toạ độ trọng tâm G của tam giác ABC theo m. Xác định m để G nằm trên đường thẳng d: { x= 1+t { y= 5-2t
Cho A(m;3) B(2;1) C(-4;5) a) tìm điều kiện của m để A,B,C là 3 đỉnh của một tam giác b) tìm toạ độ trọng tâm G của tam giác ABC theo m. Xác định m để G nằm trên đường thẳng d: { x= 1+t { y= 5-2t
Tìm giá trị thực của tham số m để parabol (P): y = m x 2 − 2mx − 3m − 2 (m ≠ 0) có đỉnh thuộc đường thẳng y = 3x − 1.
A. m = 1
B. m = -1
C. m = - 6
D. m = 6
Để đồ thị hàm số y = m x 2 − 2mx – m2 − 1 (m ≠ 0) có đỉnh nằm trên đường thẳng y = x − 2 thì m nhận giá trị nằm trong khoảng nào dưới đây?
A. (2; 6).
B. (− ∞ ; −2).
C. (0; 2).
D. (−2; 2).
Cho parabol \(\left(P\right):y=x^2+2x-3\)và đường thẳng \(\left(d\right):y=x+m\). Tìm tất cả giá trị m để (d) cắt (P) tại hai điểm phân biệt A, B nằm về hai phía của đường thẳng có phương trình y=1
Giao điểm của parabol y = x 2 + 4 x - 6 và đường thẳng y = 2x + 2 là:
A. (2; 6) và (3; 8) B. (-4; -6) và (1; -1)
C. (1; -1) và (2; 6) D. (-4; -6) và (2; 6)
Cho parabol (P): \(x^2+2x-3\) và đường thẳng d:y=x+m. Tìm m để d
cắt (P) tại hia điểm phân biệt A, B nằm về hai phía đường thẳng y=1.