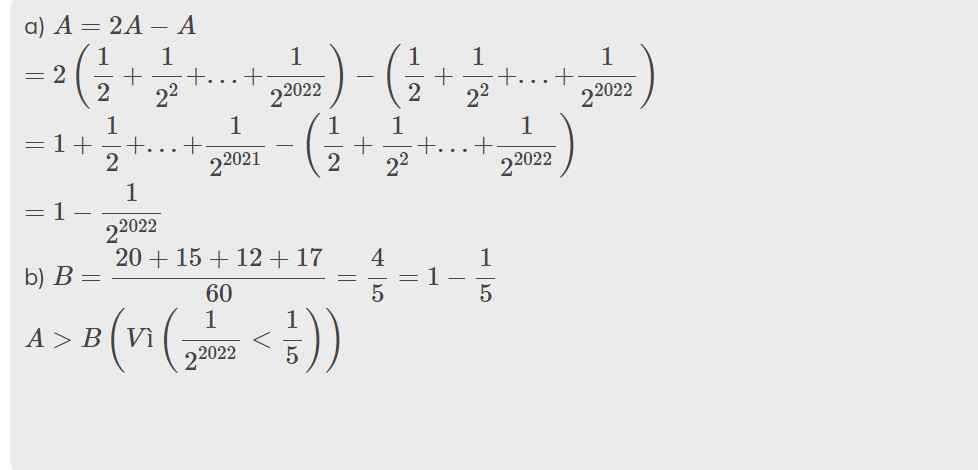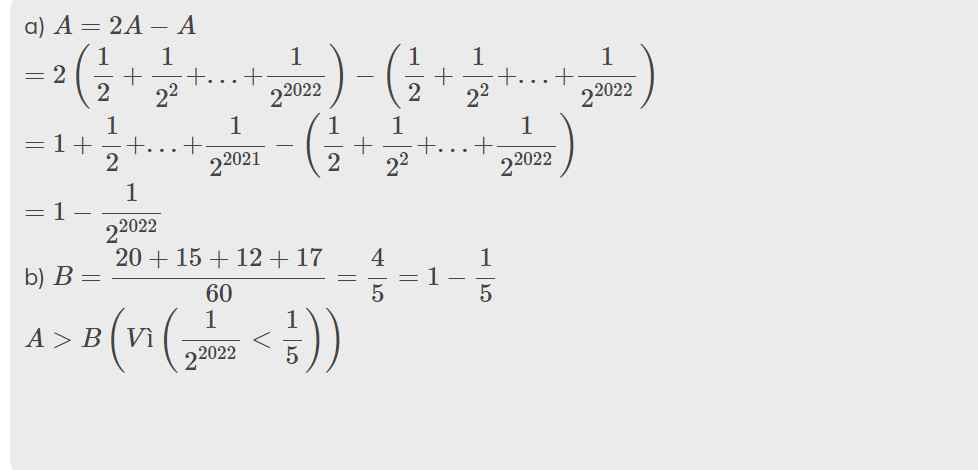\(A=2^0+2^1+2^2+...+2^{20}\)

\(2A=2^1+2^2+2^3+...+2^{21}\)

\(A=2^{21}-1\)

Vậy \(A>B\)

A=1+2+3+...+2020+2021

A=(1+2021)[(2021-1):1+1]:2

A=2043231

Có : \(S=1+2+2^2+2^3+....+2^{99}\)

\(\Rightarrow2S=2+2^2+2^3+....+2^{100}\)

\(\Rightarrow2S-S=\left(2+2^2+2^3+...+2^{100}\right)-\left(1+2+2^2+....+2^{99}\right)\)

\(\Rightarrow S=2^{100}-1< 2^{100}\)

Vậy \(S< 2^{100}\)

 S=1+2+2²+2³+....+2⁹⁹

⇒2S=2+2²+2³+....+2¹⁰⁰

⇒2S−S=2¹⁰⁰-1

S=2¹⁰⁰-1

vì 2¹⁰⁰ -1<2¹⁰⁰

⇒S<2¹⁰⁰

A=\((1+2)+\left(2^2+2^3\right)+...+\left(2^{19}+2^{20}\right)\)

A=\(3.1+2^2\left(1+2\right)+...+2^{19}\left(1+2\right)\)

A=\(3.1+3.2^2+...+3.2^{19}\)

A=\(3\left(1+2^2+...+2^{19}\right)\)\(⋮3\)

Vậy A\(⋮3\)

A=(1+2)+(22+23)+...+(219+220)(1+2)+(22+23)+...+(219+220)

A=3.1+22(1+2)+...+219(1+2)3.1+22(1+2)+...+219(1+2)

A=3.1+3.22+...+3.2193.1+3.22+...+3.219

A=3(1+22+...+219)3(1+22+...+219)⋮3⋮3

NÊN  A⋮3

Đề sai nghe

kết hợp theo công thức thì số kết thúc phải là 2¹⁹ hoặc là 2²¹  mới kết hợp được
Đừng có đánh giá người khác như thế chứ ;-;

20<21

21<22

22<23

23<24

24<25

giải ròi đó nhoa

2A=2*(1+2+2²+...+2²⁰²⁰)=2+2²+...+2²⁰²¹

^2A-A=(1+2+2²+...+2²⁰²¹)-(1+2+2²+...+2²⁰²⁰)

A=2²⁰²¹-1<2021

Giải:

A=1+2+2²+2³+...+2²⁰²⁰

2A=2+2²+2³+2⁴+...+2²⁰²¹

2A-A=(2+2²+2³+2⁴+...+2²⁰²¹)-(1+2+2²+2³+...+2²⁰²⁰)

A=2²⁰²¹-1

⇒A<2²⁰²¹

Chúc bạn học tốt!