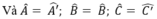Cho ΔA’B’C’ ~ ΔABC. Biết S A ’ B ’ C ’ = 25 49 S A B C và hiệu 2 chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác?
A. C A ’ B ’ C ’ = 30 m , C A B C = 46 m
B. C A ’ B ’ C ’ = 56 m , C A B C = 40 m
C. C A ’ B ’ C ’ = 24 m , C A B C = 40 m
D. C A ’ B ’ C ’ = 40 m , C A B C = 56 m