Phương trình x = a vô nghiệm với:
A.a > 0
B.a = 0
C.a < 0
D. mọi a
Cho biểu thức:
A= x^2- 2x
Tìm x để:
a.A>0:
b.A<0:
c.A=0
Cho phương trình x2-2x-\(\dfrac{a}{b}\)-\(\dfrac{b}{a}\)+3=0 với a và b là các số dương.Điều kiện để phương trình có hai nghiệm phân biệt là
A.a≠b B.a=b C.a<b D.a>b
A = 1/3 - [(-5/4 ) - ( 1/4 + 3/8)]
A.A<0 B.A<1 C.A>2 D.A < 2
\(A=\dfrac{1}{3}-\left[\left(-\dfrac{5}{4}\right)-\left(\dfrac{1}{4}+\dfrac{3}{8}\right)\right]\)
\(A=\dfrac{1}{3}-\left[\dfrac{-5}{4}-\dfrac{5}{8}\right]=\dfrac{1}{3}-\left(\dfrac{-15}{8}\right)\)
\(A=\dfrac{53}{24}\)
=> A > 2
=> C là đáp án đúng
tìm hai số tự nhiên a,b sao cho a3b chia hết cho 2,3,5,9
A.a=b=0
B.a=6,b=5
C.a=3, b=0
D.a=6, b=0
`color{red}{\text{Trả lời :}}`
Đáp án là D. a = 6, b = 0. Khi a = 6 và b = 0, ta có a^3 * b = 6^3 * 0 = 0, là một số chia hết cho 2, 3, 5 và 9.
cho phương trình ax2 + bx + c = 0 vô nghiệm ( a>0)
CMR: ax2 + bx + c > 0 với mọi x thuộc R
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
Câu 3. Kết quả được viết dưới một dạng lũy thừa là:
A.am.n. B.( a + a)m.n. C.am+n. D.(a .a)m.n.
Câu 4. Gọi A là tập hợp các chữ số của số 2021 thì :
A.A = {2 ; 0 ;1}. B.A = {2 ; 0 ; 2 ; 1} C.A = {2 ; 1}. D.A = {0 ; 1}.
Câu 5. Phân tích số ra thừa số nguyên tố ta được kết quả đúng là:
A.2.4.5. B.23.5. C.5.8. D.4.10.
Câu 6. Điều kiện của x để biểu thức chia hết cho 2 là:
A. x là số tự nhiên chẵn. B. x là số tự nhiên lẻ.
C. x là số tự nhiên bất kì. D.x ∈ {0; 2 ; 4 ; 6 ; 8}.
Gọi A là giao điểm của hai đường thẳng y = x + 2 và y = 2x + 1 , tìm tọa độ của A?
A.
A(1; -3)
B.
A(3; 1)
C.
A(1; 3)
D.
A(0; 2)
1.Nếu a+b<0 và a.b>0 thì:
A.a>0 và b>0 B.a<0,b<0 C.a>0,b<0 D.a<0,b>0
Đố. Đố em biết vì sao khi a > 0 và phương trình a x 2 + b x + c = 0 vô nghiệm thì a x 2 + b x + c > 0 với mọi giá trị của x?
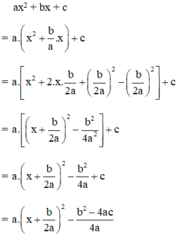
Ta có: a > 0 (gt), 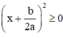 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 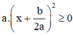
Phương trình ax2 + bx + c = 0 vô nghiệm nên
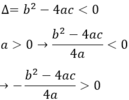
Vậy
a
x
2
+
b
x
+
c
= 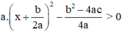 với mọi x.
với mọi x.
Đố. Đố em biết vì sao khi a > 0 và phương trình ax2 + bx + c = 0 vô nghiệm thì ax2 + bx + c > 0 với mọi giá trị của x?
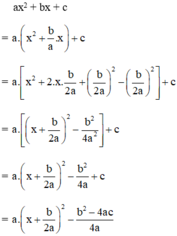
Ta có: a > 0 (gt), 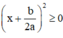 với mọi x, a, b ⇒
với mọi x, a, b ⇒ 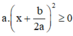
Phương trình ax2 + bx + c = 0 vô nghiệm nên
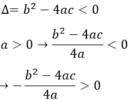
Vậy ax2 + bx + c = 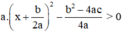 với mọi x.
với mọi x.