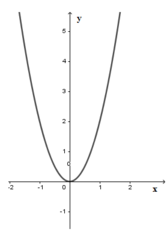
Cho đồ thị hàm số y = 2 x 2 (P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình 2 x 2 – m – 5 = 0 có hai nghiệm phân biệt.
A. m < −5
B. m > 0
C. m < 0
D. m > −5
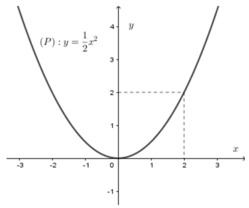
Cho đồ thị hàm số y = 1 2 x 2 (P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình x 2 – 2 m + 4 = 0 có hai nghiệm phân biệt
A. m > 2
B. m > 0
C. m < 2
D. m > −2
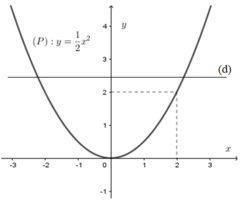
Xét phương trình x2 – 2m + 4 = 0 (*)
⇔ x2 = 2m – 4 ⇔ 1 2 x 2 = m − 2
Số nghiệm của phương trình (*) là
số giao điểm của parabol (P): y = 1 2 x 2
và đường thẳng d: y = m – 2
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
Từ đồ thị hàm số ta thấy:
Với m – 2 > 0 ⇔ m > 2 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > 2
Đáp án cần chọn là: A
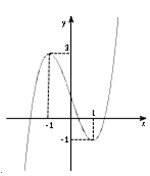
Cho đồ thị hàm số hàm y = x 3 - 3 x + 1 là hình bên. Dựa vào đồ thị hàm số đã cho hãy tìm m để phương trình y = x 3 - 3 x - m có 3 nghiệm phân biệt
A. - 1 < m < 3
B. - 2 < m < 2
C. - 2 ≤ m ≤ 2
D. - 2 ≤ m ≤ 3
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
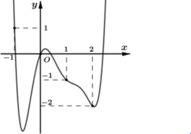
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Đáp án B
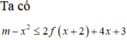
![]()
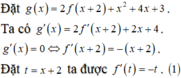
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có



Cho đồ thị hàm số y = x\(^2\) -2x - 3 :
Dựa vào đồ thị biện luận theo m số nghiệm của phương trình: x^2 - 2x - 3 + m = 0
Cho đồ thị hàm số y = f(x) có đồ thị như hình vẽ bên
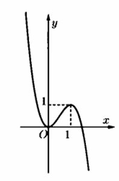
Tìm số nghiệm của phương trình f(x) = x
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Tìm m để phương trình f (x) = m có bốn ngiệm phân biệt.

A. - 4 < m < - 3
B. m > - 4
C. - 4 ≤ m < - 3
D. - 4 < m ≤ - 3
Đáp án A
PT f (x) = m có bốn nghiệm phân biệt <=> - 4 < m < - 3
a, Lập bảng biến thiên, vẽ đồ thị (P) của hàm số : y = - x^2 + 4x - 3
b, Dựa vào đồ thị, hãy:
+ Tìm x để y > 0 ; y < 0;
+ Tìm max, min của hàm số trên đoạn [0;4].
+ Biện luận theo m số nghiệm của pt x^2 - 4x = m
+Tìm k để pt -x^2 + 4x = k có nghiệm thỏa mãn [-1;3]
a: Vì a=-1<0 nên hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (-∞;2]
Bảng biến thiên là:
| x | -∞ | 2 | +∞ |
| y | -∞ | 1 | -∞ |
Cho hàm số y = - 2 x 3 + 3 x 2 - 1 có đồ thị như hình vẽ. Bằng cách sử dụng đồ thị hàm số xác định m để phương trình 2 x 3 - 3 x 2 + 2 m có đúng 3 nghiệm phân biệt, trong đó có 2 nghiệm lớn hơn 1 2
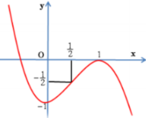
A. m ∈ - 1 2 ; 0
B. m ∈ - 1 ; 0
C. m ∈ 0 ; 1 2
D. m ∈ 1 4 ; 1 2
cho hàm số y = a/x ; a) xác định hệ số a biết đồ thị của nó đi qua điểm (-2;2) , b) vẽ đò thị hàm số đó và đường thẳng y = 2 trên cùng 1 hệ trục tọa độ Oxy ( đồ thị hàm số là đường cong hypebol) c) dựa vào đồ thị để tìm các giá trị của x sao cho 1/x<-2