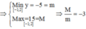Gọi M, m lần lượt là GTLN, GTNN của hàm số y = x - 1 + 7 - x . Khi đó có bao nhiêu số nguyên nằm giữa m, M ?
A. 1
B. 2
C. Vô số
D. 0
Những câu hỏi liên quan
Gọi M, m lần lượt GTLN, GTNN của hàm số
y
x
+
1
x
trên
1
3
;
3
. Khi đó 3M+m bằng: A. 12 B.
35
6
C.
7
2
D.
10
Đọc tiếp
Gọi M, m lần lượt GTLN, GTNN của hàm số y = x + 1 x trên 1 3 ; 3 . Khi đó 3M+m bằng:
A. 12
B. 35 6
C. 7 2
D. 10
Chọn A.
Trên 1 2 ; 3 ta có: y ' = 1 - 1 x 2 ; y ' = 0 ⇔ x = 1 x = - 1 L
Khi đó y 1 2 = 5 2 , y 1 = 2 , y 3 = 10 3 . Vậy: 3 M + m = 12
Đúng 0
Bình luận (0)
Gọi M và n lần lượt là gtln và gtnn của hàm số y= cos^2* x/3+ sin*x/3+1. Tính tổng M+n
Đề là \(\dfrac{cos^2x}{3}+\dfrac{sinx}{3}+1\) hay \(cos^2\left(\dfrac{x}{3}\right)+sin\left(\dfrac{x}{3}\right)+1\) vậy nhỉ?
Đúng 0
Bình luận (1)
Giả sử M, m lần lượt là GTLN, GTNN của hàm số
y
x
+
1
x
trên
1
2
;
3
. Khi đó
M
+
m
bằng bao nhiêu? A.
9
2
B.
7
2
C.
15
3...
Đọc tiếp
Giả sử M, m lần lượt là GTLN, GTNN của hàm số y = x + 1 x trên 1 2 ; 3 . Khi đó M + m bằng bao nhiêu?
A. 9 2
B. 7 2
C. 15 3
D. 16 3
Đáp án D
Ta có y ' = 1 − 1 x 2 ⇒ y ' = 0 ⇔ x = 1 x = − 1
Suy ra y 1 2 = 5 2 , y 1 = 2, y 3 = 10 3 ⇒ M = 10 3 m = 2 ⇒ M + m = 16 3
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
-
x
2
. Gọi M, m lần lượt là GTLN, GTNN của hàm số. Tính M + m A. 2 B. 4 C.
-
2 D. 0
Đọc tiếp
Cho hàm số y = x 4 - x 2 . Gọi M, m lần lượt là GTLN, GTNN của hàm số. Tính M + m
A. 2
B. 4
C. - 2
D. 0
Đáp án D
Phương pháp: Sử dụng phương pháp hàm số, tìm GTLN, GTNN của y = f(x) trên [a;b]
Bước 1: Tính f’(x) giải phương trình f’(x) = 0, tìm các nghiệm 
Bước 2: Tính các giá trị 
Bước 3: So sánh và kết luận
Cách giải:
y = x 4 - x 2
Đúng 0
Bình luận (0)
Gọi M và m lần lượt là GTLN và GTNN của hàm số
y
4
-
x
2
trên tập xác định. Khi đó
M
2
+
m
2
bằng A. 8 B. 16 C. 2 D. 4
Đọc tiếp
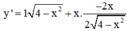
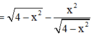
Gọi M và m lần lượt là GTLN và GTNN của hàm số y = 4 - x 2 trên tập xác định. Khi đó M 2 + m 2 bằng
A. 8
B. 16
C. 2
D. 4
Gọi M và m lần lượt là GTLN và GTNN của hàm số
y
4
−
x
2
trên tập xác định. Khi đó
M
2
+
m
2
bằng A. 2 B. 4 C. 16 D. 8
Đọc tiếp
Gọi M và m lần lượt là GTLN và GTNN của hàm số y = 4 − x 2 trên tập xác định. Khi đó M 2 + m 2 bằng
A. 2
B. 4
C. 16
D. 8
cho hàm số y= cos^2 X +4cos X + 10. Nếu M, m lần lượt là GTLN, GTNN của hàm số thì (M - m)= ?
Cho hàm số \(y=x^2-\left(m-\sqrt{m^2-16}\right)x+2m+2\sqrt{m^2-16}\) . Gọi GTLN , GTNN của hàm số trên [2:3] lần lượt là \(y_1,y_2\) . Số giá trị của tham số m để \(y_1-y_2=3\) là bao nhiêu
Gọi M và m lần lượt là GTLN và GTNN của hàm số
y
2
x
3
+
3
x
2
-
12
x
+
2
trên đoạn [
-
1;2]. Tỉ số
M
m
bằng...
Đọc tiếp
Gọi M và m lần lượt là GTLN và GTNN của hàm số y = 2 x 3 + 3 x 2 - 12 x + 2 trên đoạn [ - 1;2]. Tỉ số M m bằng
A. - 2
B. - 3
C. - 1 3
D. - 1 2
Đáp án B
Cách giải: y = 2 x 3 + 3 x 2 - 12 x + 2
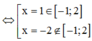
Đúng 0
Bình luận (0)