a) Với m = -2

=> hpt trở thành: \(\left\{{}\begin{matrix}x+y=2\\-2x-y=-2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}y=2-x\\-x=0\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\)

Vậy S = {0; 2}

b) Ta có: \(\left\{{}\begin{matrix}x+y=2\left(1\right)\\mx-y=m\left(2\right)\end{matrix}\right.\) 

=> x + mx = 2 + m 

<=> x(m + 1) = 2 + m

Để hpt có nghiệm duy nhất <=> \(m\ne-1\)

<=> x = \(\dfrac{m+2}{m+1}\) thay vào pt (1)

=> y = \(2-\dfrac{m+2}{m+1}=\dfrac{2m+2-m-2}{m+1}=\dfrac{m}{m+1}\)

Mà 3x - y = -10

=> \(3\cdot\dfrac{m+2}{m+1}-\dfrac{m}{m+1}=-10\)

<=> \(\dfrac{2m+6}{m+1}=-10\) <=> m + 3 = -5(m + 1)

<=> 6m = -8 

<=> m = -4/3

c) Để hpt có nghiệm <=> m \(\ne\)-1

Do x;y \(\in\) Z <=> \(\left\{{}\begin{matrix}\dfrac{m+2}{m+1}\in Z\\\dfrac{m}{m+1}\in Z\end{matrix}\right.\)

Ta có: \(x=\dfrac{m+2}{m+1}=1+\dfrac{1}{m+1}\)

Để x nguyên <=> 1 \(⋮\)m + 1

<=> m +1 \(\in\)Ư(1) = {1; -1}

<=> m \(\in\) {0; -2}

Thay vào y :

với m = 0 => y = \(\dfrac{0}{0+1}=0\)(tm)

m = -2 => y = \(\dfrac{-2}{-2+1}=2\)(tm)

Vậy ....

lỗi hình

lx hìnk còi

Đáp án B

Đáp án B

c) Hệ phương trình đã cho có nghiệm

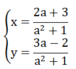
Theo đề bài : x= y

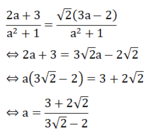
Vậy với 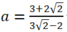 thì hệ phương trình có nghiệm (x; y) thỏa mãn x = 2 y

ĐK: x ≥ 0; y ≥ 0

Ta có

4 x − 3 y = 4 2 x + y = 2 ⇔ 4 x − 3 y = 4 4 x + 2 y = 4 ⇔ 5 y = 0 2 x + y = 2 ⇔ y = 0 2 x = 2

⇔ y = 0 x = 1 (Thỏa mãn)

Vậy hệ phương trình có 1 nghiệm duy nhất (x; y) = (1; 0) ⇒ x.y = 0

Đáp án: B

Nhân hai vế của phương trình thứ nhất với 2 rồi cộng từng vế của hai phương trình

5 x 3 + y = 2 2 x 6 − y 2 = 2 ⇔ 5 x 6 + y 2 = 4 x 6 − y 2 = 2 ⇔ 6 x 6 = 6 x 6 − y 2 = 2 ⇔ x = 1 6 1 6 . 6 − y 2 = 2 ⇔ x = 1 6 y = − 1 2

Vậy hệ đã cho có nghiệm duy nhất ( x ;   y )   =   6 6 ; − 2 2  

⇒ 6 x   +   3 3 y = 6. 6 6 + 3. 3 . − 2 2 = 6 − 3 2 6 = − 6 2

Đáp án: C

a) Ta có hệ phương trình \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\) Thay nghiệm \(\left(x,y\right)=\left(2,-1\right)\) ta có hệ mới là :

\(\hept{\begin{cases}2k-1=5\\2-1=1\end{cases}\Leftrightarrow k=3}\)

b) Ta có : \(\hept{\begin{cases}kx-y=5\\x+y=1\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=1-x\\kx-1-x=5\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}y=1-x\\x\left(k-1\right)=6\end{cases}}\)

Để hệ phương trình có nghiệm duy nhất : \(\Leftrightarrow k-1\ne0\) \(\Leftrightarrow k\ne1\)

Để hệ phương trình vô nghiệm \(\Leftrightarrow k-1=0\Leftrightarrow k=1\)

P/s : Em chưa học lớp 9 nên không biết cách trình bày cho lắm :))

b: Để hệ có nghiệm duy nhất thì \(\frac{1}{m}<>\frac{1}{-1}\)

=>m<>-1

c: Để hệ có nghiệm duy nhất thì m<>-1

\(\begin{cases}x+y=2\\ mx-y=1\end{cases}\Rightarrow\begin{cases}x+y+mx-y=2+1=3\\ x+y=2\end{cases}\)

=>\(\begin{cases}x\left(m+1\right)=3\\ x+y=2\end{cases}\Rightarrow\begin{cases}x=\frac{3}{m+1}\\ y=2-x=2-\frac{3}{m+1}=\frac{2m+2-3}{m+1}=\frac{2m-1}{m+1}\end{cases}\)

x-3y=5

=>\(\frac{3}{m+1}-\frac{3\left(2m-1\right)}{m+1}=5\)

=>3-3(2m-1)=5(m+1)

=>3-6m+3=5m+5

=>-6m+6=5m+5

=>-11m=-1

=>\(m=\frac{1}{11}\) (nhận)

d: xy<0

=>\(\frac{3}{m+1}\cdot\frac{2m-1}{m+1}<0\)

=>3(2m-1)<0

=>2m-1<0

=>\(m<\frac12\)

Kết hợp với m<>-1, ta được: \(\begin{cases}m<\frac12\\ m<>-1\end{cases}\)

e: x+2y>4

=>\(\frac{3}{m+1}+\frac{2\left(2m-1\right)}{m+1}>4\)

=>3+2(2m-1)>4(m+1)

=>3+4m-2>4m+4

=>1>4(sai)

=>m∈∅

f: Để x,y nguyên thì 3⋮m+1 và 2m-1⋮m+1

=>3⋮m+1 và 2m+2-3⋮m+1

=>3⋮m+1 và -3⋮m+1

=>3⋮m+1

=>m+1∈{1;-1;3;-3}

=>m∈{0;-2;2;-4}