(x+1)³ = 1

=> (x+1)³ = 1³

=> x+1 =1

=> x= 0

Vậy có 1 giá trị x thỏa mãn (x+1)³ =1 là x =0 

có 1 giá trị x nha 

x = 0 

( 0 + 1 )^3 = 1 

nha bạn chúc bạn học tốt nha 

x 3   –   3 x 2   +   3   -   x   =   0     ⇔   x 2 . x   –   3 . x 2   +   ( 3   –   x )   =   0     ⇔   x 2 ( x   –   3 )   –   ( x   –   3 )   =   0     ⇔   ( x   –   3 ) ( x 2   –   1 )   =   0

ó (x – 1)(x + 1)(x – 3) = 0

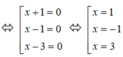
Vậy x = 1 hoặc x = 3 hoặc x = -1

Vậy có ba giá trị của x thỏa mãn đề bài

Đáp án cần chọn là:C

Có: \(\left|x-1\right|< 3\)

Mà \(\left|x-1\right|\ge0\forall x\)

\(\Rightarrow\left|x-1\right|\in\left\{0;1;2\right\}\\ \Rightarrow x-1\in\left\{0;1;-1;2;-2\right\}\\ \Rightarrow x\in\left\{1;2;0;3;-1\right\}\)

Vậy có 5 giá trị nguyên của x thỏa mãn đề bài. \(x\in\left\{x\in Z|-2< x< 4\right\}\)

Ta có: |x-1|<3

nên \(x-1\in\left\{-2;-1;0;1;2\right\}\)

hay có 5 số nguyên x thỏa mãn điều kiện |x-1|<3

Ta có

4 ( x   –   3 ) 2   –   ( 2 x   –   1 ) ( 2 x   +   1 )   =   10     ⇔   4 ( x 2   –   6 x   +   9 )   –   ( 4 x 2   –   1 )   =   10     ⇔   4 x 2   –   24 x   +   36   –   4 x 2   +   1   –   10   =   0

ó -24x + 27 = 0 ó x =   9 8

Vậy có một giá trị x thỏa mãn

Đáp án cần chọn là: C

Ta có

( 2 x   +   1 ) 2   –   4 ( x   +   3 ) 2   =   0     ⇔ 2 x 2 + 2.2 x .1 + 1 2 − 4 x 2 + 6 x + 9 = 0 ⇔   4 x 2   +   4 x   +   1   –   4 x 2   –   24 x   –   36   =   0     ⇔   - 20 x   =   35   ⇔ x = - 7 4

Vậy có một giá trị của x thỏa mãn yêu cầu.

Đáp án cần chọn là: B

\(\dfrac{x-1}{2}=\dfrac{-3}{2y+1}\)

=>\(\left(x-1\right)\cdot\left(2y+1\right)=2\cdot\left(-3\right)=-6\)

=>\(\left(x-1\right)\left(2y+1\right)=1\cdot\left(-6\right)=\left(-6\right)\cdot1=\left(-1\right)\cdot6=6\cdot\left(-1\right)=2\cdot\left(-3\right)=\left(-3\right)\cdot2=\left(-2\right)\cdot3=3\cdot\left(-2\right)\)

=>\(\left(x-1;2y+1\right)\in\left\{\left(1;-6\right);\left(-6;1\right);\left(-1;6\right);\left(6;-1\right);\left(2;-3\right);\left(-3;2\right);\left(-2;3\right);\left(3;-2\right)\right\}\)

=>\(\left(x;y\right)\in\left\{\left(2;-\dfrac{7}{2}\right);\left(-5;0\right);\left(0;\dfrac{5}{2}\right);\left(7;-1\right);\left(3;-2\right);\left(-2;\dfrac{1}{2}\right);\left(-1;1\right);\left(4;-\dfrac{3}{2}\right)\right\}\)

Với \(x\le3\) hiển nhiên ko thỏa mãn nên ta chỉ cần xét với \(x>3\)

\(\Leftrightarrow\left(x^{log_5m}+3\right)^{log_5m}=x-3\)

Đặt \(log_5m=k>1\Rightarrow\left(x^k+3\right)^k=x-3\)

Đặt \(x^k+3=t>3\Rightarrow\left\{{}\begin{matrix}x^k=t-3\\t^k=x-3\end{matrix}\right.\)

\(\Rightarrow x^k-t^k=t-x\)

\(\Rightarrow x^k+x=t^k+t\)

Hàm \(f\left(u\right)=u^k+u\) có \(f'\left(u\right)=k.u^{k-1}+1>0\Rightarrow f\left(u\right)\) đồng biến khi \(u>3\)

\(\Rightarrow x=t\)

\(\Rightarrow x^k+3=x\Rightarrow x^k-x+3=0\)

Với \(k>1\) ta có \(f\left(x\right)=x^k-x+3\) có  \(f'\left(x\right)=k.x^{k-1}-1>1.3^0-1=0\) khi \(x>3\) nên hàm đồng biến

\(\Rightarrow f\left(x\right)>f\left(3\right)=3^k>0\Rightarrow f\left(x\right)\) vô nghiệm

Vậy ko tồn tại \(m>1\) thỏa mãn yêu cầu đề bài