Giải tam giác vuông PAN vuông tại P, biết góc A bằng 320, AP = 8cm.

Những câu hỏi liên quan
Giải tam giác vuông PAN vuông tại P, biết góc A bằng 32 độ, AP = 8cm.
Góc N= 90 - 32 = 58o
PN= 8*tan32o = ?(bấm máy tính)
AN=( dùng định lí Py-ta-go)
Đúng 0
Bình luận (0)
Giải tam giác vuông: b.tam giác MAB vuông tại A, góc M = 42độ, AB=6cm. c.tam giác DEF vuông tại D,DE =8cm,góc E =32 độ d.tam giác ABC vuông tại C ,AC=7cm,góc B =30độ
Xem chi tiết
b) Ta có:
\(\widehat{B}=180^o-90^o-42^o=48^o\)
Xét tam giác ABC vuông tại A ta có:
\(cosB=\dfrac{AB}{BM}\Rightarrow cos48^o=\dfrac{6}{BM}\)
\(\Rightarrow BM=\dfrac{6}{cos48^o}\approx9\left(cm\right)\)
Mà: \(sinB=\dfrac{AM}{BM}\Rightarrow sin48^o=\dfrac{AM}{9}\)
\(\Rightarrow AM=9\cdot sin48^o\approx6,7\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có I là trung điểm của AC. Vẽ ID vuông góc với
cạnh huyền BC, (De BC).
a)Chứng minh AB2 = BD? _ CD2
b) Biết AB = 6cm; AC = 8cm. Em hãy giải tam giác vuông ABC
Nối B vs I. Xét tam giác BID vuông tại D, có:
BD2 = BI^2 - ID2 (1).Xét tam giác ICD vuông tại D, có:
DC2 = IC2 - ID2 (2).Từ (1) và (2) =>
=> BD2 - DC2
= BI2 - ID2 - IC2 + ID2
= BI2 - IC2
= BI2 - AI2 (vì AM=CM)
= AB2=> AB2 = BD2 - DC2 (đpcm)
Đúng 1
Bình luận (1)
a: \(BD^2-CD^2\)
\(=BI^2-ID^2-CI^2+ID^2=BI^2-CI^2=BI^2-AI^2=BA^2\)
b: \(CB=\sqrt{6^2+8^2}=10\left(cm\right)\)
sin B=AC/BC=4/5
=>góc B=53 độ
=>góc C=37 độ
Đúng 1
Bình luận (0)
1/ Một tam giác vuông cân có cạnh huyền bằng 2dm.Tính độ dài mỗi cạnh góc vuông2/Cho tam giác ABC có AH vuông góc với BC,AB8cm,AC13cm,HB4cm.Tính độ dài HC3/Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AH(H nằm giữa Ava2 C).Tính độ dài BC, biết HA1cm,HC8cm4/ Trên mặt phẳng tọa độ Oxy, vẽ điểm A có tọa độ(3;4). Tính độ dài OA5/Tam giác có độ dài 3 cạnh bằng$cm,7cm,8cm có là tam giác vuông hay không? Vì Sao?Mình Ko biết làm mấy bạn giúp mình với!!!!!!!!!!!!!!!!!!!!!!!!
Đọc tiếp
1/ Một tam giác vuông cân có cạnh huyền bằng 2dm.Tính độ dài mỗi cạnh góc vuông
2/Cho tam giác ABC có AH vuông góc với BC,AB=8cm,AC=13cm,HB=4cm.Tính độ dài HC
3/Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AH(H nằm giữa Ava2 C).Tính độ dài BC, biết HA=1cm,HC=8cm
4/ Trên mặt phẳng tọa độ Oxy, vẽ điểm A có tọa độ(3;4). Tính độ dài OA
5/Tam giác có độ dài 3 cạnh bằng$cm,7cm,8cm có là tam giác vuông hay không? Vì Sao?
Mình Ko biết làm mấy bạn giúp mình với!!!!!!!!!!!!!!!!!!!!!!!!
CHo tam giác ABC vuông tại A, đường caoAH. Kẻ HD vuông góc AB tại D, HE vuông góc AC tại E. Biết AB=6cm, AC=8cm. TÍnh chu vi, diện tích tam giác ADE
Cho tam giác ABC vuông tại A. Giải tam giác vuông ABC trong các trường hợp sau:
a) BC = 10cm,góc C= 30 độ. b) AB=8cm và góc B=30 độ ?
a: \(\widehat{B}=90^0-30^0=60^0\)
XétΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
nên AB=5cm
=>\(AC=5\sqrt{3}\left(cm\right)\)
b: \(\widehat{C}=90^0-30^0=60^0\)
Xét ΔABC vuông tại A có
\(\sin C=\dfrac{AB}{BC}\)
hay \(BC=16\sqrt{3}\left(cm\right)\)
=>\(AC=8\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác ABC có AB bằng 6cm, AC bằng 8cm,BC bằng 10cm.gọi AM là trung tuyến của tam giác.
a,chứng minh rằng tam giác ABC vuông tại A.
b, kẻ MD vuông góc AB, ME vuông góc AC.Tứ giác ADME là hình gì?
a) Vì AM là đường trung tuyến của BC
Mà BC=AB+AC
=> tam giác ABC vuông tại A (đpcm)
b) Xét tứ giác ADME có:
^BAC=90 độ (ABC_|_ tại A)
^MDA=90 độ (MD_|_AB)
^MEA=90 độ (ME_|_AC)
=> ADME là hcn ( 3 góc vuông )
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
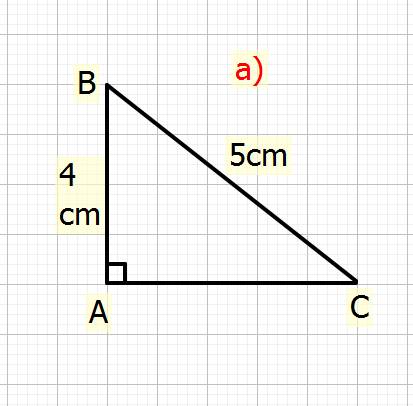
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
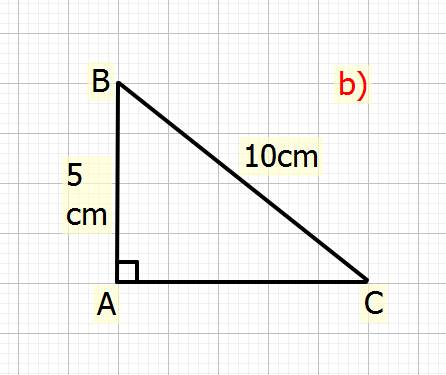
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)
Giải tam giác vuông ABC vuông tại A, biết AC = 8cm và C = 30°
\(\widehat{B}=60^0\)
BC=16cm
\(AB=8\sqrt{3}\left(cm\right)\)
Đúng 1
Bình luận (0)



















