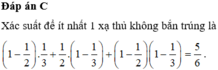Có 100 tờ vé số, có 5 tờ trúng, cho 1 người phụ nữ bốc 2 lần
a. Tính xác suất và phủ định cả 2 lần đều trúng
B. Tính xs và phủ định có ít nhất 1 lần trúng

Những câu hỏi liên quan
Có 100 tờ vé số trong đó có 20 vé trúng thưởng 50 ngàn, 10 vé trúng thưởng 100 ngàn, 5 vé trúng thưởng 150 ngàn và 65 vé không trúng thưởng. Xác suất để mua 4 vé trúng thưởng được 200 ngàn bằng:
A. 8320/156849
B. 28663/261415
C. 12060/156849
D. 44382/784245
Ba người chơi bóng rỗ, mỗi người ném một quả xác suất ném trúng của mỗi người lần lượt là 0,5, 0,6, 0,7. Tính xác xuất trong các trường hợp sau: a) có 2 người ném trúng rỗ b) có ít nhất một người ném trúng rổ
Ba xạ thủ cùng bắn vào bia. Xác suất người thứ nhất, người thứ hai, người thứ ba bắn trúng bia lần lượt là 0,8; 0,7 và 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng bia. A. 0,97 B. 0,03 C. 0,22 D. 1
Đọc tiếp
Ba xạ thủ cùng bắn vào bia. Xác suất người thứ nhất, người thứ hai, người thứ ba bắn trúng bia lần lượt là 0,8; 0,7 và 0,5. Tính xác suất để có ít nhất một xạ thủ bắn trúng bia.
A. 0,97
B. 0,03
C. 0,22
D. 1
Trong 100 vé số có 5 vé trúng. Một người mua 15 vé. Xác suất để người đó trúng 2 vé là bao nhiêu?
A. 14%
B. 20%
C. 10%
D. 23%
Đáp án A
Mua 15 vé trong 100 vé có C 15 3 cách => n ( Ω ) = C 15 3 .
Gọi X là biến cố “người đó trúng 2 vé”
Mua 2 vé trúng trong 5 vé trúng có C 5 2 cách, mua 13 vé còn lại trong 95 vé có C 95 13 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n ( X ) = C 5 2 . C 95 13
Vậy xác suất cần tính P = n ( X ) n ( Ω ) = C 5 2 . C 95 13 C 100 15 ≈ 14 % .
Đúng 0
Bình luận (0)
Trong 100 vé số có 5 vé trúng. Một người mua 15 vé. Xác suất để người đó trúng 2 vé là bao nhiêu?
A. 14%
B. 20%
C. 10%
D. 23%
Đáp án A
Mua 15 vé trong 100 vé có C 100 15 cách ⇒ n Ω = C 100 15
Gọi X là biến cố “người đó trúng 2 vé”
Mua 2 vé trúng trong 5 vé trúng có C 5 2 cách, mua 13 vé còn lại trong 95 vé có C 95 13 cách
Suy ra số kết quả thuận lợi cho biến cố X là n X = C 5 2 . C 95 13
Vậy xác suất cần tính P = n X n Ω = C 5 2 . C 95 13 C 100 15 ≈ 14 %
Đúng 0
Bình luận (0)
Hai xạ thủ cùng bắn mỗi nhười một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3
b) Tính xác suất của biến cố Y:”có ít nhất một xạ thủ không bắn trúng bia”
A. 1/2
B. 1/3
C. 1/6
D. 5/6
Gọi A là biến cố “Xạ thủ thứ i bắn trúng bia”, i=1,2
TH1. Xạ thủ thứ nhất bắn trúng, xạ thủ 2 bắn trượt thì xác suất là:
P A 1 = 1 2 . 1 − 1 3
TH2. Xạ thủ thứ nhất bắn trượt, xạ thủ thứ 2 bắn trúng thì xác suất là:
P A 2 = 1 − 1 2 . 1 3
TH3. Cả 2 xạ thủ đều bắn trượt
P A 3 = 1 − 1 2 . 1 − 1 3
Xác suất của biến cố Y là:
P Y = P A 1 + P A 2 + P A 3 = 5 6
Đáp án. D
Đúng 0
Bình luận (0)
Trong 100 vé số có 2 vé trúng. Một người mua 12 vé số. Xác suất để người đó không trúng số là bao nhiêu?
A. 75%
B. 76%
C. 77%
D. 78%
Đáp án C.
Không gian mẫu: ![]()
Gọi biến cố A là: “Người đó không trúng vé nào”
![]()
Xác suất của biến cố A là ![]()
Đúng 0
Bình luận (0)
Trong 100 vé số có 2 vé trúng. Một người mua 12 vé số. Xác suất để người đó không trúng số là bao nhiêu?
A. 75%
B. 76%
C. 77%
D. 78%
Không gian mẫu: Ω = C 100 12
Gọi biến cố A là: “Người đó không trúng vé nào”
n A = C 98 12
Xác suất của biến cố A là P A ≈ 77 %
Đúng 0
Bình luận (0)
có 3 khách hàng may mắn tham gia bốc thăm trúng thưởng đặc biệt 1 chiếc ô tô có tất cả 3 que thăm để bốc và chỉ có 1 que thăm trúng thưởng tính xác suất nhận được ô tô của người bốc thăm đầu tiên người bốc thăm thứ 2 và thứ 3
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một các độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 12 và 13. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia. A.
1
2
B.
1
3
C.
5
6
D.
2
3
Đọc tiếp
Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một các độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 12 và 13. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia.
A. 1 2
B. 1 3
C. 5 6
D. 2 3