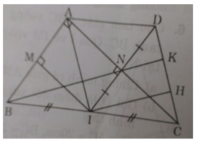
Cho ΔABC vuông tại A ( AB > AC ) . Gọi M , N lần lượt là trung điểm của AB , BC . Kẻ NP vuông góc với AC tại P. Gọi Q đối xứng với N qua M
a / Chứng minh : Tứ giác AMNP là hình chữ nhật .
b / Chứng minh : Tứ giác MNCP là hình bình hành .
c / Gọi Q đối xứng với N qua M. Chứng minh : Tứ giác AQBN là hình thoi .
d / AH là đường cao tam giác ABC . Chứng minh AH vuông góc MR .