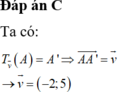Trong mặt phẳng Oxy cho vecto v = (1;2) và điểm (2;5). Tìm tọa độ ảnh của điểm M qua phép tịnh tiến vecto v

Những câu hỏi liên quan
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x(1,2), vecto y(3,4), vecto z(5,-1). Tọa độ vecto u 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4...
Đọc tiếp
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
Trong mặt phẳng tọa độ oxy cho các vecto u = (-2;1) và vecto v = 3i - mj tìm m để hai vecto u và vecto v cùng phương
Xem chi tiết
\(\overrightarrow{v}=\left(3;-m\right)\)
Hai vecto đã cho cùng phương khi và chỉ khi:
\(\dfrac{3}{-2}=\dfrac{-m}{1}\Leftrightarrow m=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng 2x - y + 1 0. Để phép tịnh tiến theo vecto
v
→
biến đường thẳng d thành chính nó thì
v
→
phải là vecto nào trong các vecto sau? A. (1;2) B. (2;-1) C. (2;1) D. (0;1)
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng 2x - y + 1 = 0. Để phép tịnh tiến theo vecto v → biến đường thẳng d thành chính nó thì v → phải là vecto nào trong các vecto sau?
A. (1;2)
B. (2;-1)
C. (2;1)
D. (0;1)
Đáp án A
Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là u d → = ( 1 ; 2 )
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng
d
:
2
x
−
y
+
1
0
. Để phép tịnh tiến theo vecto
v
⇀
biến đường thẳng d thành chính nó thì
v
⇀
phải là vecto nào trong các vecto sau? A.
2
;
−
1
B. ...
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng d : 2 x − y + 1 = 0 . Để phép tịnh tiến theo vecto v ⇀ biến đường thẳng d thành chính nó thì v ⇀ phải là vecto nào trong các vecto sau?
A. 2 ; − 1
B. 1 ; 2
C. 0 ; 1
D. 2 ; 1
Đáp án B
Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là u d → = 1 ; 2 .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình
2
x
+
y
−
1
0
. Để phép tịnh tiến theo vecto
v
→
biến d thành chính nó thì
v
→
là vecto nào trong các vecto sau? A.
v
→
2
;
1...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 2 x + y − 1 = 0 . Để phép tịnh tiến theo vecto v → biến d thành chính nó thì v → là vecto nào trong các vecto sau?
A. v → = 2 ; 1
B. v → = 1 ; 2
C. v → = - 2 ; 1
D. v → = - 1 ; 2
Đáp án D
(d) biến thành chính nó khi vecto tịnh tiến cùng phương với (d). Mà (d) có một VTCP là 1 ; 2
Đúng 0
Bình luận (0)
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto overrightarrow{a}left(1;-4right), overrightarrow{b}left(0;2right). tọa độ của vecto overrightarrow{u}2overrightarrow{a}-overrightarrow{b} là?(2) trong mặt phẳng tọa độ Oxy, cho hai vecto overrightarrow{a}left(-7;3right), overrightarrow{b}left(4;1right). tọa độ của vecto overrightarrow{u}overrightarrow{b}-2overrightarrow{a} là?(3) trong mặt phẳng tọa độ Oxy, cho hai vecto overrightarrow{u}left(-5;4right), overrightarrow{v}-3overrightarrow{j}. tọa độ c...
Đọc tiếp
(1) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(1;-4\right)\), \(\overrightarrow{b}=\left(0;2\right)\). tọa độ của vecto \(\overrightarrow{u}=2\overrightarrow{a}-\overrightarrow{b}\) là?
(2) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{a}=\left(-7;3\right)\), \(\overrightarrow{b}=\left(4;1\right)\). tọa độ của vecto \(\overrightarrow{u}=\overrightarrow{b}-2\overrightarrow{a}\) là?
(3) trong mặt phẳng tọa độ Oxy, cho hai vecto \(\overrightarrow{u}=\left(-5;4\right)\), \(\overrightarrow{v}=-3\overrightarrow{j}\). tọa độ của vecto \(\overrightarrow{a}=2\overrightarrow{u}-5\overrightarrow{v}\) là?
(4) trong mặt phẳng tọa độ Oxy, cho hai điểm A (1;1), B (4;-7) và \(\overrightarrow{OM}=2\overrightarrow{OA}-5\overrightarrow{OB}\). tổng hoành độ và tung độ của điểm M là?
giúp mk vs ạ mk cần gấp thank
(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho đường thẳng d : 2 x - y + 1 = 0 . Để phép tịnh tiến theo vecto v → biến đường thẳng d thành chính nó thì phải là vecto nào trong các vecto sau?
A. (1;2)
B. (2;-1)
C. (2;1)
D. (0;1)
Đáp án A
Vecto tịnh tiến cùng phương với d. Một vecto chỉ phương của d là ![]()
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho các vecto, vecto u=(-2,1) và vecto v=3vecto i -m vecto j. Tìm m để hai vecto u,v cùng phương
\(\overrightarrow{v}=3\overrightarrow{i}-m\overrightarrow{j}\Rightarrow\overrightarrow{v}=\left(3;-m\right)\)
Để \(\overrightarrow{u};\overrightarrow{v}\) cùng phương:
\(\Leftrightarrow\frac{3}{-2}=\frac{-m}{1}\Rightarrow m=\frac{3}{2}\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto
v
→
biến điểm A(3;-1) thành điểm A(1;4). Tìm tọa độ của vecto
v
→
? A.
v
→
(-4;3) B.
v
→
(4;3) C.
v
→
(-2;5) D.
v
→
(5;-2)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → biến điểm A(3;-1) thành điểm A'(1;4). Tìm tọa độ của vecto v → ?
A. v → =(-4;3)
B. v → =(4;3)
C. v → =(-2;5)
D. v → =(5;-2)
trong mặt phẳng tọa độ Oxy cho hai vecto a=( 1;-2) vecto b=(-1;-3). tính cos (vecto a; vecto b)
\(cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{1\cdot\left(-1\right)+\left(-2\right)\cdot\left(-3\right)}{\sqrt{1^2+2^2}\cdot\sqrt{1^2+3^2}}=\dfrac{5}{\sqrt{5}\cdot\sqrt{10}}=\dfrac{5}{\sqrt{50}}=\dfrac{1}{\sqrt{2}}\)
Đúng 0
Bình luận (0)