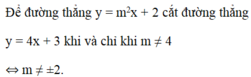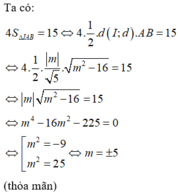Tìm tất cả giá trị thực của m để đường thẳng \(y=m^2x+2\) cắt đường thẳng y=4x+3

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của m để đường thẳng y
m
2
x + 2 cắt đường thẳng y 4x + 3. A.
m
±
2
B.
m
≠
±
2
C.
m
≠
2
D.
m
≠
−
2
Đọc tiếp
Tìm tất cả các giá trị thực của m để đường thẳng y = m 2 x + 2 cắt đường thẳng y = 4x + 3.
A. m = ± 2
B. m ≠ ± 2
C. m ≠ 2
D. m ≠ − 2
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y (3m + 2)x -7m – 1 vuông góc với đường thẳng
(
∆
)
:
y
2
x
-
1
A. m 0. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y = (3m + 2)x -7m – 1 vuông góc với đường thẳng ( ∆ ) : y = 2 x - 1
A. m = 0.
B. ![]()
C. ![]()
D. 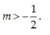
Để đường thẳng (d) vuông góc với đường thẳng ![]() thì 2(3m + 2) = -1 hay:
thì 2(3m + 2) = -1 hay:
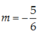
Chọn B.
Đúng 0
Bình luận (0)
Cho parabol (p):y=-2x^2 và đường thẳng (d):y=(m+1)x-m-3 (m là tham số).tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt (p) tại điểm có hoành độ =-1
Thay x=-1 vào (P), ta được:
y=-2*(-1)^2=-2
Thay x=-1và y=-2 vào (d), ta được:
-(m+1)-m-3=-2
=>-m-1-m-3=-2
=>-2m-4=-2
=>2m+4=2
=>m=-1
Đúng 1
Bình luận (0)
Tìm tổng tất cả các giá trị thực của tham số
m sao cho đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
\(y=2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x.\) song song đường thẳng y= -4x
.
Chứng minh công thức tổng quát phương trình đi qua 2 điểm cực trị:
giả sử hàm bậc 3: \(y=ax^3+bxx^2+cx+d\left(a\ne0\right)\) có 2 điểm cực trị x1;x2
Ta đi tìm số dư 1 cách tổng quát:
Ta có: \(y'=3ax^2+2bx+c-và-y''=6ax+b\)
Xét phép chia giữa y' và y'' ta có: \(y=y'\left(\dfrac{1}{3}x+\dfrac{b}{9a}\right)+g\left(x\right)\left(1\right)\) là phường trình đi qua 2 điểm cực trị của đồ thị hàm số bậc 3
từ (1) Ta có: \(y=y'\dfrac{3ax+b}{9a}+g\left(x\right)-hay-y=y'\dfrac{6ax+2b}{18a}g\left(x\right)\)
Từ đây dễ suy ra: \(g\left(x\right)=y-\dfrac{y'.y''}{18a}\left(công-thức-tổng-quát\right)\) ( dĩ nhiên bạn chỉ cần nhớ cái này )
áp dụng vào bài toán ta có:
\(2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x-\left(6x^2+6\left(m-1\right)x+6m\left(1-2m\right)\right).\dfrac{12x+6\left(m-1\right)}{18.2}\)
Gán: \(\left\{{}\begin{matrix}x=i\\m=10\end{matrix}\right.\) => 1710-841i
\(\Rightarrow y=4m\left(-2m-1\right)x+17m^2+m\) bài toán quay trở về bài toán đơn giản bạn giải nốt là oke
Đúng 1
Bình luận (2)
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
y
x
3
-
3
x
+
2
cắt đường thẳng
y
m
-
1
tại 3 điểm phân biệt A.
1
≤
m
≤
5
B.
1
m
5
C.
1
≤
m
5
D.
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 3 - 3 x + 2 cắt đường thẳng y = m - 1 tại 3 điểm phân biệt
A. 1 ≤ m ≤ 5
B. 1 < m < 5
C. 1 ≤ m < 5
D. 1 < m ≤ 5
Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = (3m + 2)x − 7m − 1 vuông góc với đường △ : y = 2x − 1.
A. m = 0
B. m = - 5 6
C. m < 5 6
D. m > - 1 2
Tìm tất cả các giá trị thực của m để đường thẳng yx+m-1 cắt đồ thị hàm số
y
2
x
+
1
x
+
1
tại hai điểm phân biệt A, B sao cho
A
B
2
3
A.
m
2
±
10
B.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của m để đường thẳng y=x+m-1 cắt đồ thị hàm số y = 2 x + 1 x + 1 tại hai điểm phân biệt A, B sao cho A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 3
C. m = 2 ± 3
D. m = 4 ± 10
Tìm tất cả các giá trị thực của m để đường thẳng y x+ m-1 cắt đồ thị hàm số
y
2
x
+
1
x
+
1
tại hai điểm phân biệt A, B sao cho
A
B
2
3
A.
m
2
±
10
B.
m
4
±...
Đọc tiếp
Tìm tất cả các giá trị thực của m để đường thẳng y= x+ m-1 cắt đồ thị hàm số y = 2 x + 1 x + 1 tại hai điểm phân biệt A, B sao cho A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 3
C. m = 2 ± 3
D. m = 4 ± 10
Phương trình hoành độ giao điểm của ( C) và d là
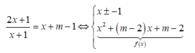
Để ( C) cắt ( d) tại hai điểm phân biệt khi và chỉ khi f( x) =0 có hai nghiệm phân biệt
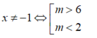
Gọi A( x1; y1) ; B( x2; y2) là giao điểm của ( C) và d
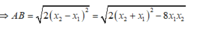
Theo hệ thức Viet, ta được
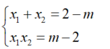
mà
![]()
Chọn D.
Đúng 0
Bình luận (0)
Tất cả các giá trị thực của tham số m để đường thẳng
d
:
y
2
x
+
m
cắt đồ thị hàm số
y
2
x
-
4
x
-
1
tại hai điểm phân biệt A và B sao cho
4
S
∆
I
A...
Đọc tiếp
Tất cả các giá trị thực của tham số m để đường thẳng d : y = 2 x + m cắt đồ thị hàm số y = 2 x - 4 x - 1 tại hai điểm phân biệt A và B sao cho 4 S ∆ I A B = 15 , với I là giao điểm của hai đường tiệm cận của đồ thị (C) là
A. m = ± 5
B. m = 0
C. m = 5
D. m = - 5