Phương trình hoành độ giao điểm của ( C) và d là
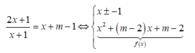
Để ( C) cắt ( d) tại hai điểm phân biệt khi và chỉ khi f( x) =0 có hai nghiệm phân biệt
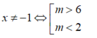
Gọi A( x1; y1) ; B( x2; y2) là giao điểm của ( C) và d
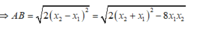
Theo hệ thức Viet, ta được
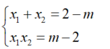
mà
![]()
Chọn D.
Phương trình hoành độ giao điểm của ( C) và d là
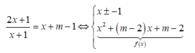
Để ( C) cắt ( d) tại hai điểm phân biệt khi và chỉ khi f( x) =0 có hai nghiệm phân biệt
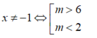
Gọi A( x1; y1) ; B( x2; y2) là giao điểm của ( C) và d
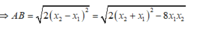
Theo hệ thức Viet, ta được
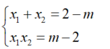
mà
![]()
Chọn D.
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y= x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 10
C. m = 4 ± 3
D. m = 2 ± 3
Tìm tất cả các giá trị của m để đường thẳng d: y=x+4 cắt đồ thị hàm số y = x 3 + 2 m x 2 + m + 3 x + 4 tại 3 điểm phân biệt A(0;4), B và C sao cho diện tích tam giác MBC bằng 4, với M(1;3)
A. m = 2 m = 3
B. m = - 2 m = 3
C. m = 3
D. m = − 3 m = − 2
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 3 - 3 ( m + 1 ) x 2 + 6 m x có hai điểm cực trị A , B sao cho đường thẳng AB vuông góc với đường thẳng : y = x + 2 .
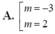

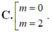
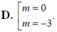
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=2x3-3( m+1) x2+ 6mx có hai điểm cực trị A; B sao cho đường thẳng AB vuông góc với đường thẳng y= x+ 2.
A. 0; 3
B. 2; 4
C. 0; 2
D. 1; 3
Tính tổng tất cả các giá trị của m biết đồ thị hàm số y = x 3 - 2 mx 2 + ( m + 2 ) x + 4 và đường thẳng y = x + 4 cắt nhau tại 3 điểm phân biệt A(0;4), B, C sao cho diện tích tam giác IBC bằng 8 2 với I(1;3)
A.3
B. 8
C. 1
D. 5
Tìm tất cả các giá trị thực của tham số m để đường thẳng y= - mx cắt đồ thị của hàm số y= x3- 3x2-m+ 2 tại ba điểm phân biệt A; B; C sao cho AB= BC.
A. m< 1
B. m> 2
C. m < 3
D. m> 4
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) và đường thẳng d: y = x + m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho AB = 10 là:
A. m = -1 hoặc m = 6
B. 0 ≤ m ≤ 5
C. m = 0 hoặc m = 6
D. m = 0 hoặc m = 7