Chọn C.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d
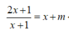
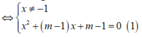
Khi đó d cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác -1
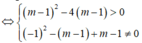
![]()
Ta có
![]()
![]()
![]()
Và 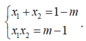
Từ đây ta có
![]()
![]()
![]()
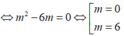 ( thỏa mãn *)
( thỏa mãn *)
Vậy chọn m = 0 hoặc m = 6
Chọn C.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d
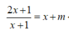
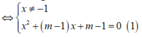
Khi đó d cắt (C) tại hai điểm phân biệt A, B khi và chỉ khi phương trình (1) có hai nghiệm phân biệt khác -1
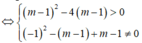
![]()
Ta có
![]()
![]()
![]()
Và 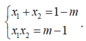
Từ đây ta có
![]()
![]()
![]()
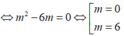 ( thỏa mãn *)
( thỏa mãn *)
Vậy chọn m = 0 hoặc m = 6
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) . Tìm tất cả các giá trị thực của tham m số sao cho đường thẳng d: y= x+m-1 cắt (C) tại hai điểm phân biệt A; B thỏa mãn A B = 2 3
A. m = 2 ± 10
B. m = 4 ± 10
C. m = 4 ± 3
D. m = 2 ± 3
Cho hàm số có đồ thị (C) y = 2 x + 1 x - 1 và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
A.m=1
B.m=1 hoặc m=5
C.m=5
D.m=-5
Cho hàm số \(y=\dfrac{1}{2}x^4-x^2+m\)(m là tham số ) có đồ thị (Cm), đường tròn (S)có phương trình \(x^2+y^2+2x+6y+1=0\) và điểm A(-1;-6).Tìm m để tồn tại tiếp tuyến với đồ thị (Cm) cắt đường tròn (S) tại hai điểm phân biệt B,C sao cho tam giác ABC có chu vi đạt giá trị lớn nhất
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) và d : y = x + m . Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
A. Không tồn tại.
B. m = 0
C. m = -3
D. m = 3
Cho hàm số y = 2 x + 1 x + 1 có đồ thị C và d: y= x+ m. Giá trị của tham số m để d cắt C tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.
A. m=6
B. m= 0
C. m= -3
D. Đáp án khác
Giả sử m = - a b , a , b ∈ ℤ * , ( a , b ) = 1 là giá trị thực của tham số m để đường thẳng d : y = - 3 x + m cắt đồ thị hàm số y = 2 x + 1 x - 1 (C) tại hai điểm phân biệt A,B sao cho trọng tâm tam giác OAB thuộc đường thẳng ∆ : x - 2 y - 2 = 0 với O là gốc tọa độ. Tính a+2b.
A. 2
B. 5
C. 11
D. 21
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()