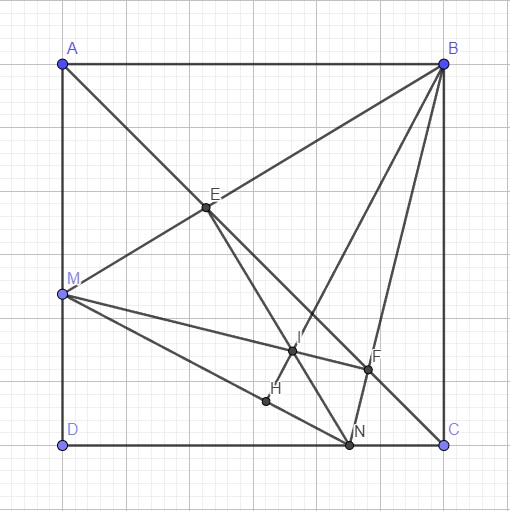
cho hình vuông ABCD có cạnh =a trên canhj AB,AD lấy 2 điểm E,F sao cho tg AEF=2a. Cm góc ECF=45 độ

Những câu hỏi liên quan
bài 1 cho tam giác ABC vuông tại A đường phân giác AD , gọi E,F lần lượt là hình chiếu của D trên AB và AC . CM tứ giác ADEF là hình vuôngbài 2 cho hình vuông ABCD có góc Agóc D 90 độ , DC2AB2AD . Kẻ BD vuông góc DC ( K thuộc DC)a, CM tứ giác ABKD là hình vuôngbài 3 cho hình vuông ABCD , có cạnh 4cm , lấy điểm E trên BC , điểm F trên CD sao cho góc EAF 45 . Trên tiaa đối của tia DC lấy K sao cho DKBEa, tính góc KAFb, tính chu vi tam giác CEF
Đọc tiếp
bài 1 cho tam giác ABC vuông tại A đường phân giác AD , gọi E,F lần lượt là hình chiếu của D trên AB và AC . CM tứ giác ADEF là hình vuông
bài 2 cho hình vuông ABCD có góc A=góc D = 90 độ , DC=2AB=2AD . Kẻ BD vuông góc DC ( K thuộc DC)
a, CM tứ giác ABKD là hình vuông
bài 3 cho hình vuông ABCD , có cạnh 4cm , lấy điểm E trên BC , điểm F trên CD sao cho góc EAF = 45 . Trên tiaa đối của tia DC lấy K sao cho DK=BE
a, tính góc KAF
b, tính chu vi tam giác CEF
Bài 1:
Do E là hình chiếu của D trên AB:
=) DE\(\perp\)AB tại E
=) \(\widehat{DE\text{A}}\)=900
Do F là hình chiếu của D trên AC:
=) DF\(\perp\)AC
=) \(\widehat{DFA}\)=900
Xét tứ giác AEDF có :
\(\widehat{D\text{E}F}\)=\(\widehat{E\text{A}F}\)=\(\widehat{DFA}\) (cùng bằng 900)
=) Tứ giác AEDF là hình chữ nhật
Xét hình chữ nhật AEDF có :
AD là tia phân giác của \(\widehat{E\text{A}F}\)
=) AEDF là hình vuông
Đúng 0
Bình luận (0)
cho cạnh hình vuông ABCD có độ dài là 1. trên các canh AB,AD lấy điểm P,Q sao cho chu vi = 2. CM góc PCQ = 45 độ
a,Dựng hình:_ Lấy 1 điểm Q bất kì thuộc cạnh AD
_Nối QC.Xác định điểm P thuộc AB sao cho góc PCQ = 45*
_Ta được tam giác APQ có chu vi bằng 2
Chứng minh:Trên tia đối của tia BA lấy điểm K sao cho BK=QD
Ta có:tam giác QDC=tam giác KBC (c-g-c)
=>QC=KC(2 cạnh tương ứng)
góc QCD = góc BCK (2 góc tương ứng)=>góc PCK = 45* và = góc QCP (theo cách vẽ)
tam giác QCP = tam giác KCP (c-g-c)
=> QP=PK (2 cạnh tương ứng)
Chu vi tam giác APQ = AP+PQ+QA=AP+PK+QA=AP+PB+QD+QA=2AB=2
b,Ta chứng minh ngược lại với câu a:
Trên tia đối của tia BA lấy điểm K sao cho BK=QD
tam giác QDC= tam giác KBC (c-g-c)
=>QC=KC(2 cạnh tương ứng)
tam giác QPC = tam giác KPC (c-c-c)
=>góc QPC= góc PCB + góc BCK=góc PCB+ gócQCD =45*
Đúng 0
Bình luận (0)
Cho cạnh hình vuông ABCD có độ dài cạnh là 1 .Trên cạnh AB,AD lấy các điểm P,Q sao cho chu vi tgAPQ bằng 2.CM góc PCQ bằng 45 độ.
ta có AB+AD=AP+PB+AQ+QD=1+1=2 mà AQ+QP+AP=2
PB+QD=QP . (*1)
Trên tia đối của BA lấy E sao cho BE=QD (*2) .
Từ (*1)(*2) có PB+BE=QP hay PE=QP
Xét 2 tam giác vuông BEC và DQC có :
BC=DC
BE=QD
tam giác BEC= tam giác DQC ( 2 cạnh góc vuông )(*****!) CE=CQ
xát tam giác QCP và tam giác ECP có :
QC=CE (c/m trên)
chung cạnh CP
QP=PE
tam giác QCP= tam giác ECP (c.c.c) góc QCP=góc PCE (***$)
Từ (*****!) có góc QCD= góc BCE mà QCD+QCB=90* nên QCB+BCE=90* hay góc QCE=90*
Đúng 0
Bình luận (0)
Cho cạnh hình vuông ABCD có độ dài là 1 cm. Trên các cạnh AB, AD lấy các điểm P, Q sao cho chu vi hình tam giác APQ = 2 cm.
Chứng minh rằng: góc PCQ = 45 độ.
Hạ CH vuông góc PQ. Vẽ hình vuông BCEF. Trên BF lấy M sao cho PM = PQ (1)
Ta có : AP + PQ + QA = 2 = AP + PM + MF => MF = QA
=> BM = 1 - MF = 1 - QA = QD
=> tg vuông BCM = tg vuông DCQ ( vì BC = DC = 1; BM = QD) => CM = CQ (2)
Từ (1) và (2) => tg CPM = tg CPQ ( vì có CP chung; PM = PQ; CM = CQ) => ^CPH = ^CPB => tg vuông CPH = tg vuông CPB => ^PCH = ^PCB (3) và CH = CB = 1; PH = PB => QH = BM ( vì PQ = PM) => tg vuông CQH = tg vuông BMC = tg vuông DCQ => ^DCQ = ^HCQ (4)
Từ (3) và (4) => ^PCQ = ^PCH + ^HCQ = ^PCB + ^DCQ = 90o - ^PCQ => 2^PCQ = 90o => ^PCQ = 45 do
nho cho minh 1 tick nha
Đúng 0
Bình luận (0)
Hạ CH vuông góc PQ. Vẽ hình vuông BCEF. Trên BF lấy M sao cho PM = PQ (1)
Ta có : AP + PQ + QA = 2 = AP + PM + MF => MF = QA
=> BM = 1 - MF = 1 - QA = QD
=> tg vuông BCM = tg vuông DCQ ( vì BC = DC = 1; BM = QD) => CM = CQ (2)
Từ (1) và (2) => tg CPM = tg CPQ ( vì có CP chung; PM = PQ; CM = CQ) => ^CPH = ^CPB => tg vuông CPH = tg vuông CPB => ^PCH = ^PCB (3) và CH = CB = 1; PH = PB => QH = BM ( vì PQ = PM) => tg vuông CQH = tg vuông BMC = tg vuông DCQ => ^DCQ = ^HCQ (4)
Từ (3) và (4) => ^PCQ = ^PCH + ^HCQ = ^PCB + ^DCQ = 90o - ^PCQ => 2^PCQ = 90o => ^PCQ = 45o
Đúng 0
Bình luận (0)
Hạ CH vuông góc PQ. Vẽ hình vuông BCEF. Trên BF lấy M sao cho PM = PQ (1)
Ta có : AP + PQ + QA = 2 = AP + PM + MF => MF = QA
=> BM = 1 - MF = 1 - QA = QD
=> tg vuông BCM = tg vuông DCQ ( vì BC = DC = 1; BM = QD) => CM = CQ (2)
Từ (1) và (2) => tg CPM = tg CPQ ( vì có CP chung; PM = PQ; CM = CQ) => ^CPH = ^CPB => tg vuông CPH = tg vuông CPB => ^PCH = ^PCB (3) và CH = CB = 1; PH = PB => QH = BM ( vì PQ = PM) => tg vuông CQH = tg vuông BMC = tg vuông DCQ => ^DCQ = ^HCQ (4)
Từ (3) và (4) => ^PCQ = ^PCH + ^HCQ = ^PCB + ^DCQ = 90o - ^PCQ => 2^PCQ = 90o => ^PCQ = 45 °
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho hình chữ nhật ABCD (AB>BC) lấy điểm E trên cạnh AD, lấy F,K trên cạnh CD sao cho DF=CK ,(F nằm giữa D và K ) vẽ đường thẳng vuông góc với EK tại K cắt BC tại M .CM góc EFM=90 độ
1,Cho hinh thoi ABCD có chu vi 16cm. Đường chéo AC= 4cm. Tính độ dài đường chéo BD
2,Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh AC lấy điểm E sao cho AF=DE. Cm AE=BF và AE vuông góc BF
Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh CD lấy điểm E sao cho AF=DE
a, Cm ΔABF=ΔADE
b, Cm góc FAE+ góc AFB = 90o
c, Cm AE⊥BF
a: Xét ΔABF vuông tại A và ΔDAE vuông tại D có
AB=DA
AF=DE
=>ΔABF=ΔDAE
b: ΔABF=ΔDAE
=>góc ABF=góc DAE
=>góc FAE+góc AFB=90 độ
c; Gọi giao của AE và FB là O
góc FAE+góc AFB=90 độ
=>góc OAF+góc OFA=90 độ
=>AE vuông góc BF tại O
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh bằng a. Trên AB lấy E, AD lấy F sao cho AE+AF+EF=2a. Vẽ CH\(⊥\)EF. CMR:
a.H thuộc 1 đường tròn cố định.
b. Xác định E,F sao cho S AEF nhỏ nhất, lớn nhất.
Cho hình vuông ABCD cạnh có độ dài bằng a. Trên cạnh AD lấy điểm M và cạnh CD lấy điểm N sao cho góc MBN 45°. Gọi E và F lần lượt là giao điểm của BM, BN với AC.
a/ Chứng minh: Tứ giác BENC nội tiếp, từ đó suy ra NE vuông góc với BM
b/ Gọi I là giao điểm của NE và MF. Chứng minh: BI vuông góc với MN.
c/ Tìm vị trí của M và N để diện tích tam giác MDN lớn nhất. Tính diện tích lớn nhất đó theo a.
Đọc tiếp
Cho hình vuông ABCD cạnh có độ dài bằng a. Trên cạnh AD lấy điểm M và cạnh CD lấy điểm N sao cho góc MBN = 45°. Gọi E và F lần lượt là giao điểm của BM, BN với AC. a/ Chứng minh: Tứ giác BENC nội tiếp, từ đó suy ra NE vuông góc với BM b/ Gọi I là giao điểm của NE và MF. Chứng minh: BI vuông góc với MN. c/ Tìm vị trí của M và N để diện tích tam giác MDN lớn nhất. Tính diện tích lớn nhất đó theo a.
a.
DO ABCD là hình vuông \(\Rightarrow\widehat{ACD}=45^0\)
\(\Rightarrow\widehat{ACD}=\widehat{EBN}\)
Mà \(\widehat{ACD}\) và \(\widehat{EBN}\) cùng chắn EN
\(\Rightarrow\) Tứ giác BENC nội tiếp
\(\Rightarrow\widehat{BEN}+\widehat{BCN}=180^0\)
\(\Rightarrow\widehat{BEN}=180^0-\widehat{BCN}=180^0-90^0=90^0\)
\(\Rightarrow NE\perp BM\) tại E
b.
Tương tự ta có tứ giác ABFM nội tiếp (\(\widehat{MAF}=\widehat{MBF}=45^0\) cùng chắn MF)
\(\Rightarrow\widehat{BFM}+\widehat{BAM}=180^0\)
\(\Rightarrow\widehat{BFM}=90^0\Rightarrow MF\perp BN\)
\(\Rightarrow I\) là trực tâm của tam giác BMN
\(\Rightarrow BI\perp MN\)
Đúng 0
Bình luận (0)
c.
Gọi H là giao điểm BI và MN
Do E và F cùng nhìn MN dưới 1 góc vuông
\(\Rightarrow\) Tứ giác EFMN nội tiếp
\(\Rightarrow\widehat{EMN}+\widehat{EFN}=180^0\)
Mà \(\widehat{EFN}+\widehat{EFB}=180^0\)
\(\Rightarrow\widehat{EMN}=\widehat{EFB}\)
Lại có tứ giác ABFM nội tiếp (A và F cùng nhìn BM dưới 1 góc vuông)
\(\Rightarrow\widehat{EFB}=\widehat{AMB}\) (cùng chắn AB)
\(\Rightarrow\widehat{EMN}=\widehat{AMB}\)
\(\Rightarrow\Delta_VAMB=\Delta_VHMB\left(ch-gn\right)\)
\(\Rightarrow AM=HM\)
Đồng thời suy ra \(AB=BH\Rightarrow BH=BC\) (do AB=BC)
Theo Pitago: \(\left\{{}\begin{matrix}HN=\sqrt{BN^2-BH^2}\\CN=\sqrt{BN^2-BC^2}\end{matrix}\right.\) \(\Rightarrow CN=HN\)
\(\Rightarrow AM+CN=MH+NH=MN\)
\(\Rightarrow MD+DN+MN=MD+DN+AM+CN=AD+CD=2a\)
Pitago: \(MN^2=DM^2+DN^2\ge\dfrac{1}{2}\left(DM+DN\right)^2\Rightarrow MN\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a-\left(DM+DN\right)\ge\dfrac{\sqrt{2}}{2}\left(DM+DN\right)\)
\(\Rightarrow2a\ge\left(\dfrac{2+\sqrt{2}}{2}\right)\left(DM+DN\right)\ge\left(2+\sqrt{2}\right).\sqrt{DM.DN}\)
\(\Rightarrow DM.DN\le\left(6-4\sqrt{2}\right)a^2\)
\(\Rightarrow S_{MDN}=\dfrac{1}{2}DM.DN\le\left(3-2\sqrt{2}\right)a^2\)
Dấu "=" xảy ra khi \(DM=DN=\left(\sqrt{6}-\sqrt{2}\right)a\)
Đúng 0
Bình luận (0)