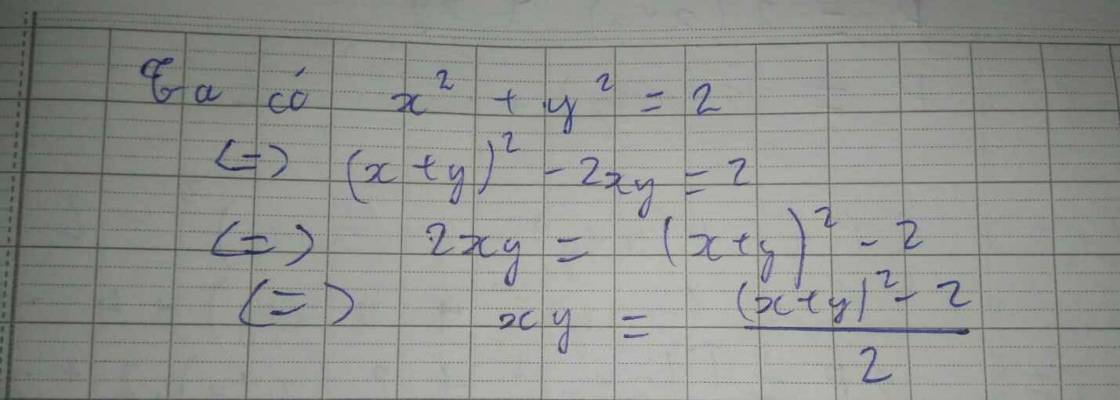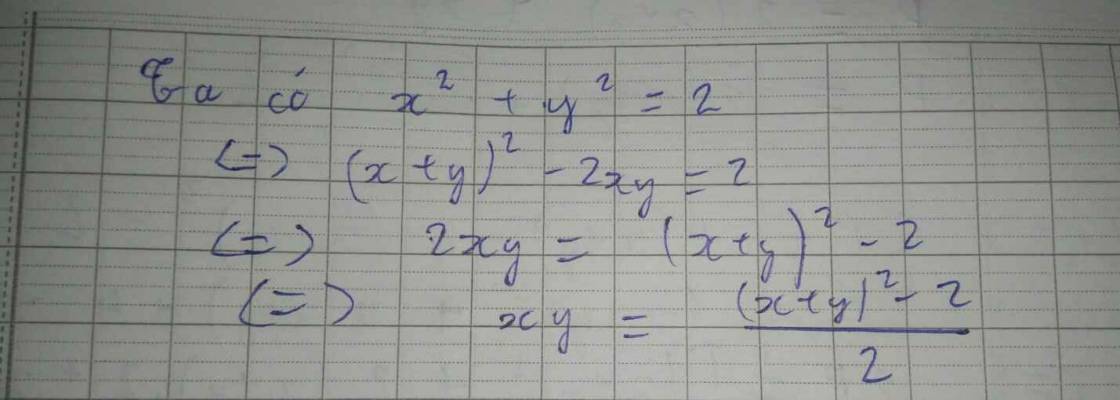Tìm x+y biết (x-2)^2 + x^2 + (y-x)^2 = 2. (x,y là số thực nhé)

Những câu hỏi liên quan
Cho x, y là các số thực TM x^2+y^2=2. Tìm MIN P=2(x+y)+xy
(Đề Dịch Vọng 22-23)
Mọi người giúp mình nhé. Thanks =)
Cho x, y là các số thực TM x^2+y^2=2. Tìm MIN P=2(x+y)+xy
(Đề Dịch Vọng 22-23)
Mọi người giúp mình nhé. Thanks =)
Tìm Min và Max của A=x^2+y^2 biết x,y là 2 số thực thỏa mãn x^2+y^2-xy=4
Tìm x, y biết :
a) 4/x=2/y
b) x/y=2/7
c) -2/x=y/3
d) x-3/y-2=3/2 với hiệu x-y=4
dấu / là phân số nhé !
Các bạn giải chi tiết nhé ! thanks !
tìm 2 số thực x,y biết x/2=y/5 và x+y=42
áp dụng t/c dtsbn ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{42}{7}=6\)
\(\dfrac{x}{2}=6\Rightarrow x=12\\ \dfrac{y}{5}=6\Rightarrow y=30\)
Đúng 1
Bình luận (0)
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{42}{7}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.6=12\\y=5.6=30\end{matrix}\right.\)
Đúng 2
Bình luận (0)
4. tìm số tự nhiên x và y, biết rằng:
a) x.(y - 2 ) = 8
b) ( x - 1 ).( y - 2 )= 9
c) ( x + 1 ) . ( y - 2 ) = 15
Mơn nhé ^ ^
\(a,x\left(y-2\right)=8\\ \Rightarrow x;\left(y-2\right)\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y-2\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) | \(8\) | \(4\) | \(2\) | \(1\) |
| \(y\) | \(1\) | \(0\) | \(-2\) | \(-6\) | \(10\) | \(6\) | \(4\) | \(3\) |
Vậy \(\left(x;y\right)=\left(-8;1\right),\left(-4;0\right),\left(-2;-2\right),\left(-1;-6\right),\left(2;6\right),\left(4;4\right),\left(8;3\right)\)
Đúng 1
Bình luận (0)
\(b,\left(x-1\right)\left(y-2\right)=9\\ \Rightarrow\left(x-1\right),\left(y-2\right)\inƯ\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\)
| \(x-1\) | \(-9\) | \(-3\) | \(-1\) | \(1\) | \(3\) | \(9\) |
| \(y-2\) | \(-1\) | \(-3\) | \(-9\) | \(9\) | \(3\) | \(1\) |
| \(x\) | \(-8\) | \(-2\) | \(0\) | \(2\) | \(4\) | \(10\) |
| \(y\) | \(1\) | \(-1\) | \(-7\) | \(11\) | \(5\) | \(3\) |
Vậy \(\left(x;y\right)=\left(-8;1\right),\left(-2;-1\right),\left(0;-7\right),\left(2;11\right),\left(4;5\right),\left(10;3\right)\)
Đúng 1
Bình luận (1)
\(c,\left(x+1\right)\left(y-2\right)=15\\ \Rightarrow\left(x+1\right),\left(y-2\right)\inƯ\left(15\right)=\left\{-15;-1;1;15\right\}\)
| \(x+1\) | \(-15\) | \(-1\) | \(1\) | \(15\) |
| \(y-2\) | \(-1\) | \(-15\) | \(15\) | \(1\) |
| \(x\) | \(-16\) | \(-2\) | \(0\) | \(14\) |
| \(y\) | \(1\) | \(-13\) | \(17\) | \(3\) |
Vậy \(\left(x;y\right)=\left(-16;1\right),\left(-2;-13\right),\left(0;17\right),\left(14;3\right)\)
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực # 0. Tìm x,y,z là số thực # 0 thỏa mãn x*y/a*y+b*x=y*z/b*z+c*y=z*x/c*x+a*z=(x^2+y^2+z^2)/(a^2+b^2+c^2)
tìm tất cả các số thực x,y biết
x^2+y^2=128 và x^2-y^2=(căn y-căn x ).(x+y+2014)
cho a,b,c là các số thực # 0. Tìm các số thực x,y,z #0 thỏa mãn: x*y/a*y+b*x=y*z/b*z+c*y=z*x/c*x+a*z=(x^2+y^2+z^2)/(a^2+b^2+c^2)