giúp mình với

Các số được điền vào các ô theo thứ tự từ trái sang phải là:

-1; - \(\dfrac{1}{3}\);  \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

Vì nếu andehit là RCHO thì số mol của nó phải là 0,2 mol. Suy ra số mol của ancol = 0,2 mol.

Mà ancol sinh ra từ phản ứng:

R(COOR')2 + 2NaOH ---> R(COONa)2 + 2R'OH

Do đó số mol R(COONa)2 = 0,1 mol. Nên khi nung với CaO thì thu được ankan cũng có số mol = 0,1 mol > 0,08 điều này là vô lí.

Bài 5:

a: AE là phân giác của góc BAC

=>\(\hat{BAE}=\hat{CAE}=\frac12\cdot\hat{BAC}\)

Xét ΔAEC có \(\hat{AEB}\) là góc ngoài tại đỉnh E

nên \(\hat{AEB}=\hat{EAC}+\hat{ECA}\)

\(=\frac12\cdot\hat{BAC}+\hat{ACB}=\frac12\left(180^0-\hat{ABC}-\hat{ACB}\right)+\hat{ACB}=90^0-\frac12\cdot\hat{ACB}-\frac12\cdot\hat{ABC}+\hat{ACB}\)

\(=90^0-\frac12\cdot\hat{ABC}+\frac12\cdot\hat{ACB}=90^0-\frac12\left(\hat{ABC}-\hat{ACB}\right)\)

b: BK//AE
=>\(\hat{ABK}=\hat{BAE}\) (hai góc so le trong) và \(\hat{AKB}=\hat{EAC}\) (hai góc đồng vị)

mà \(\hat{BAE}=\hat{EAC}\) (AE là phân giác của góc BAC)

nên \(\hat{ABK}=\hat{AKB}\)

=>ΔABK có hai góc bằng nhau

Bài 6:

a: AM//BD

=>\(\hat{BMA}=\hat{CBD}\) (hai góc đồng vị) và \(\hat{BAM}=\hat{ABD}\) (hai góc so le trong)

mà \(\hat{CBD}=\hat{ABD}\) (BD là phân giác của góc ABC)

nên \(\hat{BMA}=\hat{BAM}\)

b: ΔBAM có \(\hat{BAM}=\hat{BMA}\)

nên ΔBAM cân tại B

ΔBAM cân tại B

mà BI là đường phân giác

nên BI⊥AM

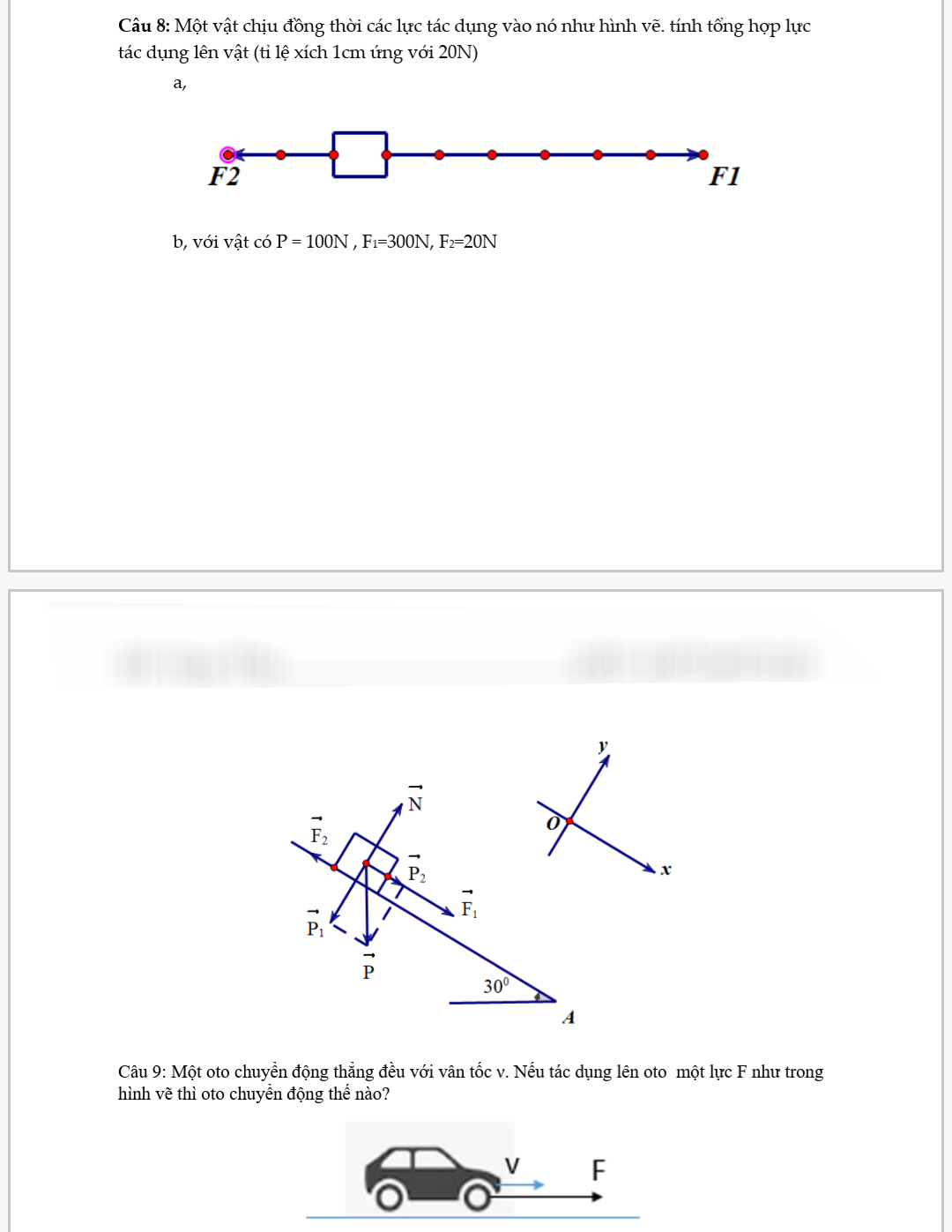
Bạn nên đăng những câu khó nhất hoặc bạn lọc ra những câu tương tự nhau để bản thân có thể vận dụng nhé!

0;2;4;6;8

0, 2, 4, 6, 8

Bài 1:

\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)

Bài 2:

\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)

Bài 3:

\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)

Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)

Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)

\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)

Bài 4:

\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)